Análisis de red de correlaciones ponderadas

Redes de correlación ponderadas

 Wikipedia




El análisis de red de correlación ponderada, también conocido como análisis de red de coexpresión de genes ponderados (WGCNA), es un método de minería de datos ampliamente utilizado, especialmente para el estudio de redes biológicas basadas en correlaciones de pares entre variables. Si bien se puede aplicar a la mayoría de los conjuntos de datos de alta dimensión, se ha utilizado más ampliamente en aplicaciones genómicas. Permite definir módulos (clústeres), concentradores intramodulares y nodos de red con respecto a la pertenencia a módulos, estudiar las relaciones entre los módulos de coexpresión y comparar la topología de red de diferentes redes (análisis diferencial de redes). El WGCNA se puede usar como una técnica de reducción de datos (relacionada con el análisis factorial oblicuo), como un método de agrupamiento (agrupamiento difuso), como un método de selección de características (por ejemplo, como método de detección de genes), como marco para integrar datos complementarios (genómicos) ( basado en correlaciones ponderadas entre variables cuantitativas) y como una técnica de exploración de datos. [1] Aunque WGCNA incorpora técnicas tradicionales de exploración de datos, su lenguaje de red intuitivo y su marco de análisis trascienden cualquier técnica de análisis estándar. Debido a que utiliza una metodología de red y es adecuada para integrar conjuntos de datos genómicos complementarios, puede interpretarse como un método de análisis de datos genéticos de sistemas biológicos o sistemas. Al seleccionar los centros intramodulares en los módulos de consenso, WGCNA también da lugar a técnicas de metanálisis basadas en redes. [2]

Historia

El método WGCNA fue desarrollado por Steve Horvath, profesor de genética humana en la Escuela de Medicina David Geffen en UCLA y de bioestadística en la Escuela de Salud Pública Fielding de la UCLA y sus colegas en la UCLA, y (ex) miembros del laboratorio (en particular Peter). Langfelder, Bin Zhang, Jun Dong). Gran parte del trabajo surgió de colaboraciones con investigadores aplicados. En particular, las redes de correlación ponderadas se desarrollaron en conversaciones conjuntas con los investigadores del cáncer Paul Mischel, Stanley F. Nelson y los neurocientíficos Daniel H. Geschwind, Michael C. Oldham (según la sección de reconocimiento en [1]). Existe una vasta literatura sobre redes de dependencia, redes de escala libre y redes de coexpresión.

Comparación entre redes de correlación ponderadas y no ponderadas

Una red de correlación ponderada puede interpretarse como un caso especial de una red ponderada, una red de dependencia o una red de correlación. El análisis de la red de correlación ponderada puede ser atractivo por los siguientes motivos.

• La construcción de la red (basada en un umbral suave del coeficiente de correlación) preserva la naturaleza continua de la información de correlación subyacente. Por ejemplo, las redes de correlación ponderadas que se construyen sobre la base de correlaciones entre variables numéricas no requieren la elección de un umbral duro. La información dicotomizante y el umbral (difícil) pueden llevar a la pérdida de información. [3]
• La construcción de la red tiene resultados altamente robustos con respecto a las diferentes opciones de umbral suave. [3] Por el contrario, los resultados basados ​​en redes no ponderadas, construidas por el umbral de una medida de asociación por pares, a menudo dependen en gran medida del umbral.
• Las redes de correlación ponderadas facilitan una interpretación geométrica basada en la interpretación angular de la correlación, capítulo 6 en. [4]
• Las estadísticas de red resultantes pueden utilizarse para mejorar los métodos estándar de extracción de datos, como el análisis de conglomerados, ya que las medidas de similitud (des) a menudo se pueden transformar en redes ponderadas; [5] ver capítulo 6 en [4].
• WGCNA proporciona estadísticas de conservación de módulos potentes que pueden usarse para cuantificar si se pueden encontrar en otra condición. Además, las estadísticas de conservación de módulos permiten estudiar las diferencias entre la estructura modular de las redes. [6]
• Las redes ponderadas y las redes de correlación a menudo se pueden aproximar mediante redes "factorizables". [4] [7] Tales aproximaciones a menudo son difíciles de lograr para redes dispersas y no ponderadas. Por lo tanto, las redes ponderadas (de correlación) permiten una parametrización parsimoniosa (en términos de módulos y membresía de módulos) (capítulos 2, 6 en [1]) y [8].

Método

Primero, uno define una medida de similitud de coexpresión de genes que se usa para definir la red. Denotamos la medida de similitud de coexpresión de genes de un par de genes i y j por . Muchos estudios de coexpresión utilizan el valor absoluto de la correlación como una medida de similitud de coexpresión sin signo,



donde los perfiles de expresión génica y consisten en la expresión de los genes i y j a través de múltiples muestras. Sin embargo, el uso del valor absoluto de la correlación puede ofuscar información biológicamente relevante, ya que no se hace distinción entre la represión de genes y la activación. En contraste, en las redes firmadas, la similitud entre los genes refleja el signo de la correlación de sus perfiles de expresión. Para definir una medida de coexpresión firmada entre los perfiles de expresión génica y , se puede usar una transformación simple de correlación:



Como la medida no firmada sijunsigned , la similitud firmada toma un valor entre 0 y 1. Tenga en cuenta que la similitud no firmada entre dos genes expresados ​​de manera opuesta ( es igual a 1 mientras que es igual a 0 para la similitud signada. De manera similar, mientras que la medida de coexpresión sin firmar de dos genes con correlación cero permanece en cero, la similitud con signo es igual a 0.5.

A continuación, se usa una matriz de adyacencia (red), , se utiliza para cuantificar la fuerza con que los genes están conectados entre sí. A se define mediante el umbral de la matriz de similitud de coexpresión . El umbral 'duro' (dicotomización) la medida de similitud S da como resultado una red de coexpresión de genes no ponderada. Específicamente, una adyacencia de red no ponderada se define como 1 si y 0 en caso contrario. Debido a que el umbral difícil codifica las conexiones genéticas de forma binaria, puede ser sensible a la elección del umbral y resultar en la pérdida de información de coexpresión. [3] La naturaleza continua de la información de coexpresión se puede preservar empleando un umbral suave, que da como resultado una red ponderada. Específicamente, WGCNA utiliza la siguiente función de potencia para evaluar la fuerza de su conexión:

,

donde la potencia β es el parámetro de umbral suave. Los valores predeterminados β = 6 y β = 12 se utilizan para redes sin firma y firmadas, respectivamente. Alternativamente, se puede elegir β utilizando el criterio de topología sin escala que equivale a elegir el valor más pequeño de β, de manera que se alcance la topología libre de escala aproximada. [3]

Dado que , la adyacencia de red ponderada está relacionada linealmente con la similitud de coexpresión en una escala logarítmica. Tenga en cuenta que un β de alta potencia transforma altas similitudes en adyacencias altas, mientras que empuja similitudes bajas hacia 0. Dado que este procedimiento de umbral suave aplicado a una matriz de correlación de pares conduce a una matriz de adyacencia ponderada, el análisis que sigue es Se denomina análisis de red de coexpresión de genes ponderados.

Un paso importante en el análisis centrado en el módulo es agrupar genes en módulos de red utilizando una medida de proximidad de red. En términos generales, un par de genes tiene una alta proximidad si está estrechamente interconectado. Por convención, la proximidad máxima entre dos genes es 1 y la proximidad mínima es 0. Normalmente, el WGCNA usa la medida de superposición topológica (TOM) como proximidad. [9] [10] que también se puede definir para redes ponderadas. [3] El TOM combina la adyacencia de dos genes y las fortalezas de conexión que estos dos genes comparten con otros genes de "terceros". El TOM es una medida altamente robusta de interconexión de red (proximidad). Esta proximidad se utiliza como entrada del agrupamiento jerárquico de enlaces promedio. Los módulos se definen como ramas del árbol de agrupamiento resultante utilizando el enfoque de corte dinámico de ramas. [11] A continuación, los genes dentro de un módulo dado se resumen con el módulo eigengene, que se puede considerar como el mejor resumen del modo estandarizado.El módulo eigengene de un módulo dado se define como el primer componente principal de los perfiles de expresión estandarizados. Los eigengenes definen biomarcadores robustos. [12] Para encontrar módulos que se relacionan con un rasgo clínico de interés, los módulos de eigengenes se correlacionan con el rasgo clínico de interés, lo que da lugar a una medida de significación de eigengene. Los eigengenes se pueden usar como características en modelos predictivos más complejos, incluidos los árboles de decisión y las redes bayesianas. [12] También se pueden construir redes de coexpresión entre módulos de eigengenes (redes de eigengene), es decir, redes cuyos nodos son módulos. [13] Para identificar los genes centrales intramodulares dentro de un módulo dado, se pueden usar dos tipos de medidas de conectividad. El primero, denominado , es definido en función de la correlación de cada gen con el respectivo módulo eigengene. El segundo, denominado kIN, se define como una suma de adyacencias con respecto a los genes del módulo. En la práctica, estas dos medidas son equivalentes. [4] Para probar si un módulo se conserva en otro conjunto de datos, se pueden usar varias estadísticas de red, por ejemplo. . [6]

Aplicaciones

WGCNA se ha utilizado ampliamente para analizar datos de expresión génica (es decir, datos de transcripción), por ej. para encontrar genes hub intramodulares. [2] [14]

A menudo se usa como un paso de reducción de datos en aplicaciones de sistemas genéticos donde los módulos están representados por "módulos eigengenes", por ejemplo [15] [16] Los eigengenes del módulo pueden usarse para correlacionar módulos con rasgos clínicos. Las redes Eigengene son redes de coexpresión entre módulos eigengenes (es decir, redes cuyos nodos son módulos). WGCNA se usa ampliamente en aplicaciones neurocientíficas, por ejemplo [17] [18] y para analizar datos genómicos, incluidos datos de micromatrices, [19] datos de RNA-Seq de células individuales [20] [21] datos de metilación del DNA, [22] datos de miRNA, conteos de péptidos [23] y datos de microbiota (secuenciación del gen 16S rRNA). 24] Otras aplicaciones incluyen datos de imágenes del cerebro, por ejemplo, datos funcionales de resonancia magnética. [25]

Paquete de software R

El paquete de software WGCNA R [26] proporciona funciones para llevar a cabo todos los aspectos del análisis de redes ponderadas (construcción de módulos, selección de genes centrales, estadísticas de conservación de módulos, análisis de redes diferenciales, estadísticas de redes). El paquete WGCNA está disponible en Comprehensive R Archive Network (CRAN), el repositorio estándar para paquetes del complemento de R.

Referencias

1. Horvath S (2011). Weighted Network Analysis: Application in Genomics and Systems Biology. New York, NY: Springer. ISBN 978-1-4419-8818-8.
2. Langfelder P, Mischel PS, Horvath S, Ravasi T (17 April 2013). "When Is Hub Gene Selection Better than Standard Meta-Analysis?". PLoS ONE. 8 (4): e61505. Bibcode:2013PLoSO...861505L. doi:10.1371/journal.pone.0061505. PMC 3629234. PMID 23613865.
3. Zhang B, Horvath S (2005). "A general framework for weighted gene co-expression network analysis" (PDF). Statistical Applications in Genetics and Molecular Biology. 4: 17. CiteSeerX 10.1.1.471.9599. doi:10.2202/1544-6115.1128. PMID 16646834.
4. Horvath S, Dong J (2008). "Geometric Interpretation of Gene Coexpression Network Analysis". PLoS Computational Biology. 4 (8): e1000117. Bibcode:2008PLSCB...4E0117H. doi:10.1371/journal.pcbi.1000117. PMC 2446438. PMID 18704157.
5. Oldham MC, Langfelder P, Horvath S (12 June 2012). "Network methods for describing sample relationships in genomic datasets: application to Huntington's disease". BMC Systems Biology. 6: 63. doi:10.1186/1752-0509-6-63. PMC 3441531. PMID 22691535. 
6. Langfelder P, Luo R, Oldham MC, Horvath S (20 January 2011). "Is my network module preserved and reproducible?". PLoS Computational Biology. 7 (1): e1001057. Bibcode:2011PLSCB...7E1057L. doi:10.1371/journal.pcbi.1001057. PMC 3024255. PMID 21283776. 
7. Dong J, Horvath S (4 June 2007). "Understanding network concepts in modules". BMC Systems Biology. 1: 24. doi:10.1186/1752-0509-1-24. PMC 3238286. PMID 17547772. 
8. Ranola JM, Langfelder P, Lange K, Horvath S (14 March 2013). "Cluster and propensity based approximation of a network". BMC Systems Biology. 7: 21. doi:10.1186/1752-0509-7-21. PMC 3663730. PMID 23497424. 
9. Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabasi AL (2002). "Hierarchical organization of modularity in metabolic networks". Science. 297 (5586): 1551–1555. arXiv:cond-mat/0209244. Bibcode:2002Sci...297.1551R. doi:10.1126/science.1073374. PMID 12202830. 
10. Yip AM, Horvath S (24 January 2007). "Gene network interconnectedness and the generalized topological overlap measure" (PDF). BMC Bioinformatics. 8: 22. doi:10.1186/1471-2105-8-22. PMC 1797055. PMID 17250769. 
11. Langfelder P, Zhang B, Horvath S (2007). "Defining clusters from a hierarchical cluster tree: the Dynamic Tree Cut library for R". Bioinformatics. 24 (5): 719–20. doi:10.1093/bioinformatics/btm563. PMID 18024473. 
12. Foroushani A, Agrahari R, Docking R, Chang L, Duns G, Hudoba M, Karsan A, Zare H (16 March 2017). "Large-scale gene network analysis reveals the significance of extracellular matrix pathway and homeobox genes in acute myeloid leukemia: an introduction to the Pigengene package and its applications". BMC Medical Genomics. 10 (1): 16. doi:10.1186/s12920-017-0253-6. PMC 5353782. PMID 28298217. 
13. Langfelder P, Horvath S (2007). "Eigengene networks for studying the relationships between co-expression modules". BMC Systems Biology. 2007 (1): 54. doi:10.1186/1752-0509-1-54. PMC 2267703. PMID 18031580. 
14. Horvath S, Zhang B, Carlson M, Lu KV, Zhu S, Felciano RM, Laurance MF, Zhao W, Shu Q, Lee Y, Scheck AC, Liau LM, Wu H, Geschwind DH, Febbo PG, Kornblum HI, Cloughesy TF, Nelson SF, Mischel PS (2006). "Analysis of Oncogenic Signaling Networks in Glioblastoma Identifies ASPM as a Novel Molecular Target". PNAS. 103 (46): 17402–17407. Bibcode:2006PNAS..10317402H. doi:10.1073/pnas.0608396103. PMC 1635024. PMID 17090670. 
15. Chen Y, Zhu J, Lum PY, Yang X, Pinto S, MacNeil DJ, Zhang C, Lamb J, Edwards S, Sieberts SK, Leonardson A, Castellini LW, Wang S, Champy MF, Zhang B, Emilsson V, Doss S, Ghazalpour A, Horvath S, Drake TA, Lusis AJ, Schadt EE (27 March 2008). "Variations in DNA elucidate molecular networks that cause disease". Nature. 452 (7186): 429–35. Bibcode:2008Natur.452..429C. doi:10.1038/nature06757. PMC 2841398. PMID 18344982. 
16. Plaisier CL, Horvath S, Huertas-Vazquez A, Cruz-Bautista I, Herrera MF, Tusie-Luna T, Aguilar-Salinas C, Pajukanta P, Storey JD (11 September 2009). "A Systems Genetics Approach Implicates USF1, FADS3, and Other Causal Candidate Genes for Familial Combined Hyperlipidemia". PLoS Genetics. 5 (9): e1000642. doi:10.1371/journal.pgen.1000642. PMC 2730565. PMID 19750004. 
17. Voineagu I, Wang X, Johnston P, Lowe JK, Tian Y, Horvath S, Mill J, Cantor RM, Blencowe BJ, Geschwind DH (25 May 2011). "Transcriptomic analysis of autistic brain reveals convergent molecular pathology". Nature. 474 (7351): 380–4. doi:10.1038/nature10110. PMC 3607626. PMID 21614001. 
18. Hawrylycz MJ, Lein ES, Guillozet-Bongaarts AL, Shen EH, Ng L, Miller JA, van de Lagemaat LN, Smith KA, Ebbert A, Riley ZL, Abajian C, Beckmann CF, Bernard A, Bertagnolli D, Boe AF, Cartagena PM, Chakravarty MM, Chapin M, Chong J, Dalley RA, David Daly B, Dang C, Datta S, Dee N, Dolbeare TA, Faber V, Feng D, Fowler DR, Goldy J, Gregor BW, Haradon Z, Haynor DR, Hohmann JG, Horvath S, Howard RE, Jeromin A, Jochim JM, Kinnunen M, Lau C, Lazarz ET, Lee C, Lemon TA, Li L, Li Y, Morris JA, Overly CC, Parker PD, Parry SE, Reding M, Royall JJ, Schulkin J, Sequeira PA, Slaughterbeck CR, Smith SC, Sodt AJ, Sunkin SM, Swanson BE, Vawter MP, Williams D, Wohnoutka P, Zielke HR, Geschwind DH, Hof PR, Smith SM, Koch C, Grant S, Jones AR (20 September 2012). "An anatomically comprehensive atlas of the adult human brain transcriptome". Nature. 489 (7416): 391–399. Bibcode:2012Natur.489..391H. doi:10.1038/nature11405. PMC 4243026. PMID 22996553. 
19. Kadarmideen HN, Watson-Haigh NS, Andronicos NM (2011). "Systems biology of ovine intestinal parasite resistance: disease gene modules and biomarkers". Molecular BioSystems. 7 (1): 235–246. doi:10.1039/C0MB00190B. PMID 21072409. 
20. Kogelman LJ, Cirera S, Zhernakova DV, Fredholm M, Franke L, Kadarmideen HN (30 September 2014). "Identification of co-expression gene networks, regulatory genes and pathways for obesity based on adipose tissue RNA Sequencing in a porcine model". BMC Medical Genomics. 7 (1): 57. doi:10.1186/1755-8794-7-57. PMC 4183073. PMID 25270054. 
21. Xue Z, Huang K, Cai C, Cai L, Jiang CY, Feng Y, Liu Z, Zeng Q, Cheng L, Sun YE, Liu JY, Horvath S, Fan G (29 August 2013). "Genetic programs in human and mouse early embryos revealed by single-cell RNA sequencing". Nature. 500 (7464): 593–7. Bibcode:2013Natur.500..593X. doi:10.1038/nature12364. PMC 4950944. PMID 23892778. 
22. Horvath S, Zhang Y, Langfelder P, Kahn RS, Boks MP, van Eijk K, van den Berg LH, Ophoff RA (3 October 2012). "Aging effects on DNA methylation modules in human brain and blood tissue". Genome Biology. 13 (10): R97. doi:10.1186/gb-2012-13-10-r97. PMC 4053733. PMID 23034122. 
23. Shirasaki DI, Greiner ER, Al-Ramahi I, Gray M, Boontheung P, Geschwind DH, Botas J, Coppola G, Horvath S, Loo JA, Yang XW (12 July 2012). "Network organization of the huntingtin proteomic interactome in mammalian brain". Neuron. 75 (1): 41–57. doi:10.1016/j.neuron.2012.05.024. PMC 3432264. PMID 22794259. 
24. Tong M, Li X, Wegener Parfrey L, Roth B, Ippoliti A, Wei B, Borneman J, McGovern DP, Frank DN, Li E, Horvath S, Knight R, Braun J (2013). "A modular organization of the human intestinal mucosal microbiota and its association with inflammatory bowel disease". PLoS One. 8 (11): e80702. Bibcode:2013PLoSO...880702T. doi:10.1371/journal.pone.0080702. PMC 3834335. PMID 24260458. 
25. Mumford JA, Horvath S, Oldham MC, Langfelder P, Geschwind DH, Poldrack RA (1 October 2010). "Detecting network modules in fMRI time series: a weighted network analysis approach". NeuroImage. 52 (4): 1465–76. doi:10.1016/j.neuroimage.2010.05.047. PMC 3632300. PMID 20553896. 
26. Langfelder P, Horvath S (29 December 2008). "WGCNA: an R package for weighted correlation network analysis". BMC Bioinformatics. 9: 559. doi:10.1186/1471-2105-9-559. PMC 2631488. PMID 19114008.

Interpretando la evolución de precios a través de una red de correlaciones

Características de la estructura de correlación de los índices de precios
Xiangyun Gao, Haizhong An y Weiqiong Zhong


PLoS One. 2013; 8(4): e61091.
Published online 2013 Apr 8. doi: 10.1371/journal.pone.0061091

Resumen
¿Cuáles son las características de la estructura de correlación de los índices de precios? Para responder a esta pregunta, se seleccionaron como datos de muestra 5 tipos de índices de precios, incluyendo 195 índices de precios específicos de 2003 a 2011. Para construir una red ponderada de índices de precios cada índice de precios está representado por un vértice, y una correlación positiva entre dos índices de precios está representada por una arista. Estudiamos las características de la estructura de red ponderada aplicando la teoría económica al análisis de parámetros de red complejos. Se encontró que la frecuencia de los índices de precios sigue una distribución normal contando los grados ponderados de los nodos e identificamos los índices de precios que tienen un impacto importante en la estructura de la red. Encontramos grupos pequeños en la red ponderada por los métodos de k-core y k-plex. Descubrimos huecos de estructura en la red calculando la jerarquía de los nodos. Finalmente, encontramos que la red ponderada de índices de precios tiene un efecto de pequeño mundo calculando el camino más corto. Estos resultados proporcionan una base científica para las políticas de control macroeconómico.

Introducción

Los índices de precios son indicadores importantes para medir la inflación y el desarrollo económico. El gobierno influye en los precios de los productos básicos por una variedad de políticas reguladoras para mantener la estabilidad del mercado. Los índices de precios incluyen el índice de precios al consumidor (IPC) de los residentes, el índice de precios al productor (IPP), el índice de precios al por menor (RPI), el índice de precios de la producción agrícola y del material de producción agrícola y las materias primas, Índice de precios de compra (RFPPI) [1] - [9]. Estos 5 tipos de índices de precios se dividen en muchos índices de precios específicos. Por ejemplo, en China, el IPC se clasifica en ocho categorías: alimentos, tabaco y licor, ropa, equipo y servicios domésticos, productos de salud y personales, transporte y comunicaciones, entretenimiento y productos educativos y servicios y vivienda. Estos 5 tipos de índices de precios se obtienen calculando índices de precios específicos con pesos. Por lo tanto, en comparación con el IPC, PPI, RPI, API y RFPPI, los índices de precios específicos reflejan más directamente los cambios en los precios de los productos básicos. Por esta razón, estudiamos índices de precios específicos en lugar de estos 5 tipos de índices de precios.

Hay relaciones entre los índices de precios que se han encontrado en la investigación anterior. Modelos y métodos de econometría se aplican para probar que hay relaciones causales [4], relaciones de cointegración [5], relaciones interactivas [10] y relaciones de transmisión [11] - [13] entre los 5 índices de precios. Estas relaciones se basan en la correlación entre los índices de precios [14]. Sin embargo, hay muchos índices de precios específicos para cada tipo, entre los que las relaciones desconcertantes forman una red complicada [15] - [17]. En esta red de índices de precios, ¿cuáles índices de precios tienen un mayor impacto? ¿Cómo se afectan entre sí? Cuando uno de ellos cambia, ¿cuáles son los índices de precios que transmitirán el impacto de la fluctuación? ¿Hasta dónde puede llegar el proceso de transmisión y cuál es el camino de transmisión? Debido a que los modelos econométricos tradicionales no pueden incluir tantos índices de precios, si lo hacemos, el modelo será demasiado difícil de usar [14]. Para responder a las 4 preguntas anteriores, primero debemos averiguar las características de la estructura de relación entre los índices de precios. La teoría de la red compleja puede resolver eficazmente los problemas relativos a las características de la estructura de la relación. El concepto central de teoría de red compleja es ver la relación entre las variables en el sistema real como una red compleja, describir la relación entre las variables en el sistema complejo real en forma de red y obtener una mejor comprensión de Su naturaleza analizando la estructura del sistema [18] - [20]. Esta teoría proporciona un enfoque adecuado para analizar cuantitativamente el comportamiento de las redes complejas en el sistema económico, como el fenómeno del mundo pequeño [16], [21]. La diversidad de las relaciones de los individuos está fuertemente correlacionada con el desarrollo económico de las comunidades [22]. Los investigadores han analizado las relaciones de los individuos entre los índices bursátiles basados ​​en la red de correlación. Descubrieron las características de la volatilidad y las existencias dominantes en los índices bursátiles [23], [24], [25]. En el sistema económico, cientos de índices de precios interactúan y se afectan entre sí, y la estructura de correlación forma una red compleja. Así, podemos analizar la estructura de correlación por la teoría de la red compleja.

Materiales y métodos

Materiales

En el presente estudio se recopilaron datos sobre índices de precios específicos de 2003 a 2011 del país en desarrollo China (Anuario Estadístico de China, 2003-2011). Se utilizaron los datos de los cinco tipos de índices de precios siguientes: IPC, RPI, API, PPI y RFPPI. Cada índice de precios se divide en índices de precios específicos, con un total de 195 índices. Los principales elementos de los diversos tipos de índices de precios se muestran en el cuadro 1, por ejemplo, el índice de precios de los alimentos incluye un índice de precios de los alimentos, un índice de precios del petróleo, un índice de precios de carne y aves, Índices de precios.

Tabla 1

Principales elementos de los índices de precios.

Tipo de índice de precios		Elementos principales
Índice de Precios al Consumidor (CPI)	Alimentos, Tabaco, Licor y Artículos, Vestuario, Instalaciones Domésticas, Artículos y Servicios, Cuidado de la Salud y Artículos Personales, Transporte y Comunicación, Recreación, Educación y Cultura Artículos, Residencia, et al.
Índice de precios al por menor (RPI)	Bebidas, Tabaco y Licor, Ropa, Calzado y Sombreros, Textiles, Electrodomésticos, Equipo de Música y Video, Instrumentos Musicales y de Oficina, Artículos de Uso Diario, Artículos de Deportes y Recreación, Plata y Joyería, Medicina Tradicional China y Occidental y Artículos de Salud, Libros, Periódicos, Revistas y Publicaciones Electrónicas, Combustibles, Materiales de Construcción y Ferretería, et al.
Índice de precios al productor de bienes manufacturados (PPI)	Industria metalúrgica, industria del petróleo, electrodomésticos, equipo de música y video, industria de fabricación de máquinas, industria de materiales de construcción, industria maderera, industria alimentaria, industria textil, industria de la confección, industria del cuero, industria del papel, Artículos Educativos y Artesanales, et al.
Índice de Precios de Productos Agrícolas y Índice de Precios de Material Productivo Agrícola (API)	Fertilizantes Químicos, Fertilizantes Químicos, Plaguicidas y sus Aparatos, Petróleo para Maquinaria Agrícola, Otros Productos de la Ganadería, Productos de la Pesca, Productos Farmacéuticos Medios de Producción Agrícola, Servicio de Producción Agrícola, et al.
Índice de precios de compra de materias primas, combustible y energía (RFPPI)	Combustible y energía, Metales ferrosos, Metales no ferrosos, Materias primas químicas, Electrodomésticos, Equipo de música y video, Materiales de construcción, Productos agrícolas, Materiales textiles, et al.

Redes ponderadas de índices de precios

Para estudiar las características de la estructura de correlación de índices de precios específicos, primero debemos establecer la red ponderada por el índice de precios (PIWN) por la teoría de redes complejas. Una red es una colección de nodos y enlaces, N = (V, E). Representamos cada índice de precios como un vértice, y representamos la relación entre dos índices de precios como un borde en la red; Por lo tanto, volvimos el estudio de la estructura de correlación de los índices de precios en un estudio de una compleja red de correlaciones de precios.

El conjunto de vértices V en la red compleja de correlaciones de índices de precios se expresa como

      (1)

Donde vi representa el i-ésimo índice de precios.

El conjunto de nodos E en la red compleja de correlaciones de índices de precios se expresa como

       (2)

Donde e(i, j) representa la relación entre el i-ésimo índice de precios y el j-ésimo índice de precios.

En el curso de este estudio, se intentó definir y cuantificar la relevancia de la red. Cuantificamos el enla ce e(i, j)  y usamos el coeficiente de correlación rij para representar el grado de correlación entre el i-ésimo índice de precios y el j-ésimo índice de precios. El coeficiente de correlación, también conocido como el coeficiente de correlación de Pearson, es un indicador que mide el grado de correlación entre las tendencias cambiantes de las variables, con un rango de [-1,1]. Cuanto mayor sea el valor absoluto del coeficiente de correlación, mayor será el grado de correlación entre las variables.

          (3)

Donde im es el valor de la serie temporal del i-ésimo índice de precios, un archivo externo que  es el valor promedio de la serie temporal del i-ésimo índice de precios,  jn es el valor de la serie temporal del índice de precios j-th,  es el valor medio de la serie temporal del índice de precios j-ésimo, y s es el número de elementos de la serie de índices de precios.

Así, la matriz de coeficientes de correlación del índice de precios R se forma como

           (4)

Si todos los coeficientes de correlación se reflejan en la red con pesos, entonces la red está completamente conectada y no está disponible para el análisis de topología. Además, para establecer con mayor exactitud la relación y la estructura entre los índices de precios, debemos eliminar las correlaciones débiles y las no correlaciones estableciendo un umbral. El PIWN es una red basada en umbrales, y como todas las redes basadas en umbral, es muy sensible al valor del umbral. Los bordes cuyo peso sea menor que el valor umbral pueden omitirse [23], [24]. A medida que el umbral aumenta, la red se vuelve más informativa sobre la estructura de correlación parcial del sistema, pero la selección de correlación parcial podría verse afectada por la incertidumbre estadística. No se supone que el valor de umbral sea demasiado bajo. En las redes económicas, el umbral suele establecerse por encima de 0,7 [23], [25].

Las propiedades topológicas y métricas del PIWN dependen fuertemente del valor del coeficiente de correlación r. Para seleccionar un valor adecuado para r, iterativamente elegir diferentes valores de este coeficiente de correlación y calcular la suma de los pesos de todos los bordes en el PIWN resultante. Representamos esta cantidad como E (r).

Para r = 0,7, tenemos E (0,7) = 3734. Presentamos la fracción  como una función de r. Además, realizamos un análisis similar para el tamaño del componente conectado más grande de la red, dependiendo del valor de r. Se indica el número total de vértices en la mayor componente conectada de la PIWN para un r dado con V (r). En la figura 1, mostramos la cantidad , donde r = 0,82 es el punto de ruptura. Por lo tanto, elegimos 0,82 como nuestro valor umbral para el tamaño de un gran componente conectado y no trivial topológica y métrica propiedades de la red resultante índice de precios [24]. Si el coeficiente de correlación entre dos índices de precios no es inferior a 0,82, entonces hay una ventaja entre ellos. El valor del coeficiente de correlación entre dos índices de precios se establece como el peso del borde. Así, construimos un modelo de estructura de red compleja y ponderada de fuertes correlaciones de índices de precios, como se muestra en la Figura 2.

Dos medidas de conectividad PIWN en función del parámetro r.
El valor r = 0,82 es la medida utilizada en este trabajo.

Red compleja de correlaciones fuertes de índices de precios.
Los 4 nodos azules son nodos aislados que no tienen una fuerte correlación con otros nodos.

Resultados

Las 4 preguntas sobre el PIWN mencionadas anteriormente son manejadas por el método de análisis paramétrico de red compleja, incluyendo el grado ponderado, k-core, k-plex, la jerarquía de los agujeros estructurales y el camino más corto.

Índices de precios clave

¿Qué índices de precios tienen un mayor impacto? Para responder a esta pregunta, debemos encontrar los índices clave de precios en el PIWN. Los índices clave de precios son los indicadores que tienen un impacto muy alto en el PIWN; Cuanto mayor sea el grado ponderado de un nodo, más amplio será su impacto. En los sistemas económicos, cuanto más amplio es el impacto de un índice, más importante es en la red. Por lo tanto, podemos encontrar índices clave de precios en el PIWN calculando el grado ponderado de los nodos. El grado ponderado de un nodo es la suma de todos los valores ponderados de sus bordes. Esta suma no sólo incluye el número de índices de precios relacionados con el nodo sino que también considera el grado de sus correlaciones. El grado ponderado WDi de un índice de precios (vértice) i se define como

                       (5)

Donde r es el valor del coeficiente de correlación entre los vértices i y los vértices j. En la figura 2, cuanto mayor sea el valor, mayor será el nodo en la red.

Nuestro experimento incluye 191 nodos y 1.795 enlaces en el PIWN. Se calculó el grado ponderado de los 191 nodos, se reflejó a nivel macro, y se encontró que, en toda la estructura de la red de correlación de índices de precios, el grado de influencia del PPI es el más amplio. Así, a nivel macro, PPI es el índice de precios clave. El IPP se refiere al índice de precios al productor en China. En estudios sobre la relación de transmisión de precios en la cadena industrial, muchos estudiosos creen que el PPI puede usarse para representar el nivel de precios en la cadena de transmisión de la industria. En segundo lugar, el grado de influencia del IPC es del 24%, y este índice puede utilizarse en lugar del precio descendente en la cadena de transmisión de la industria. Los resultados muestran que el IBP tiene un mayor impacto en la tasa de inflación que el IPC. Los resultados de otros estudios también apoyan esta conclusión. Utilizando el análisis empírico, el mecanismo de transmisión del precio de producción al precio al consumidor es más importante que el mecanismo de transmisión del precio al consumidor al precio de producción [11]. En general, las fluctuaciones del nivel general de precios aparecen en primer lugar en la zona de producción y, a partir de ahí, se extienden por las cadenas industriales hasta las industrias posteriores y, finalmente, a los bienes de consumo [12]. Por lo tanto, para controlar la tasa de inflación en China, el primero de la cadena industrial se puede considerar en primer lugar. Los resultados también muestran que el grado de influencia de la API es hasta un 15%. China es un país agrícola; Por lo tanto, no debe subestimarse el impacto del nivel de precios de la producción agrícola y su impacto en otras industrias. Especialmente en los países en desarrollo, el aumento de los costos básicos de vida de las personas a menudo tiene una serie de consecuencias, como la reciente "inflación porcina" en China. Tres tipos de índices de precios, el IPP, el IPC y el API, cubren el 80% del grado de influencia. Las estadísticas de la correlación entre los índices de precios macro se muestran en la Tabla 2, y la proporción de cada índice se muestra en la Figura 3.

Proporciones de índices de precios macro con relaciones de correlación.

Tabla 2

Grado ponderado de los índice de precios macro.

Tipo de índide de precios	Grado ponderado
PPI	1286.29
CPI	787.21
API	496.98
RPI	463.55
RFPPI	182.89

En la Tabla S1, proporcionamos todos los valores del grado ponderado del índice de precios. Hay sólo un pequeño número de índices de precios clave en el PIWN. Sólo 3 índices clave de precios tienen grados de ponderación superiores a 40. En el cuadro 3 se muestra el valor del grado ponderado del índice de precios (top 10). Este cuadro muestra que, en el sistema de índices de precios, sólo unos pocos índices de precios Tienen impactos mayores de 40. Los cambios en estos índices clave de precios darán lugar a fluctuaciones en los otros índices de precios y conducirán a algún fenómeno económico de todo el sistema. Por ejemplo, China es el país más poblado del mundo. El costo de vida del pueblo ocupa un lugar central en su desarrollo económico; Como resultado, las fluctuaciones en la vida cotidiana y la venta al por menor, los índices de precios al consumidor son a menudo la causa de la inflación [26].

Tabla 3

El valor del grado ponderado del índice de precios (top 10).

Rango	Tipo de índice de precios	Grado ponderado
1	RPI(Rural Household)	42.19
2	PPI(Articles for Daily Use)	41.70
3	RPI	40.59
4	PPI(Manufacture of General Purpose Machinery)	39.92
5	RPI(Urban Household)	39.64
6	CPI(Rural Household)	39.14
7	PPI(Manufacture of Special Purpose Machinery)	39.00
8	PPI(Manufacture of Artwork and Other Manufacturing)	38.63
9	RPI(Building Materials and Hardware)	38.58
10	PPI(Consumer Goods)	37.62

Encontramos que hay hasta 41 grados ponderados cuyo valor es inferior a 4,8. En la figura 2, los nodos en la parte escasa de la estructura de la red son pequeños, lo que significa que tienen menos impacto en comparación con otros índices de precios y permanecen en estados relativamente independientes. Al analizar los índices de precios con grados ponderados entre 4,8 y 44,8, encontramos que siguen una distribución normal, como se muestra en la Figura 4. Los papeles principales del sistema de índices de precios están ocupados por los índices medios, índices de precios con grados ponderados entre 8,8 y 32,8. Estos resultados pueden usarse como una referencia para decidir las direcciones claves para la regulación de la inflación en China. Sin embargo, en el PIWN general, hay algunos grupos de grupos relativamente independientes y un medio de transmisión entre los índices de precios que deben estudiarse más.


Figura 4
Distribución del índice de precios

Agrupamientos de grupos de precios

¿Cómo se afectan los índices de precios entre ellos? Para responder a esta pregunta, debemos estudiar los grupos de grupo en el PIWN. Los clusters de grupos son sub-redes en las que los índices de precios tienen fuertes correlaciones. En un sistema económico real, muchos índices de precios de los productos básicos interactúan entre sí. Los cambios en un índice de precios tienden a impulsar cambios en otro índice de precios; Existe una relación mutuamente fuerte entre estos índices de precios. Como se observa en la Figura 2, toda la red incluye algunos pequeños grupos de grupos de red, que están en un estado relativamente independiente. Descubrimos que los grupos de índices de precios pueden ayudarnos a comprender las características de la estructura de correlación de los índices de precios y proporcionar mejores referencias para el control de las políticas. El k-plex y el método k-core se basan en el descubrimiento de grados de vértice en subgrupos; Son útiles para identificar pequeños grupos de clusters en la estructura de red del índice de precios. Utilizando el método de descubrimiento de subgrupos, se aprovechan los clústeres de grupos en el índice de precios, lo que puede ayudar al intentar comprender qué otros índices cambian cuando cambia un índice de precios específico.

El método k-plex requiere que cada vértice de los g vértices que están incluidos en un subgrupo mantiene al menos g-k enlaces con otros vértices en el mismo subgrupo, donde k es un coeficiente de ajuste; Cuanto menor sea el valor de k, mayor será el valor de g. Además, cuanto más exigentes sean las condiciones, más estrecha será la relación entre los vértices. El método k-core se refiere a un subgrafo con las siguientes condiciones: los puntos en el subgrafo son al menos adyacentes a k otros puntos en el subgrafo. El método k-plex requiere que, además del punto k, los puntos estén conectados con al menos un punto fuera de los k puntos, mientras que el método k-core requiere que cada punto esté conectado a al menos k puntos.

Primero, use el método k-core para encontrar k-core en el PIWN. Los resultados experimentales muestran que hay 18 grupos de grupos (Figura 5 muestra diferentes colores que representan diferentes k-núcleos). Hay siete grupos con escalas de vértices de no menos de 10 (la escala de vértices representa el número de índices de precios en un grupo de grupos), como se muestra en la Figura 6. Los clusters de grupos más grandes contienen 42 índices de precios. Como se muestra en la Figura 5, hay 3 agrupaciones de grupos grandes en el PIWN, incluyendo el 43% de los índices de precios y el 54% de las correlaciones. Estos grupos de 3 grupos están en posiciones significativas; Cualquier índice de precios en los cambios del grupo de clusters despertará cambios en los otros y dará lugar a cambios en el conjunto. Así, el gobierno podría controlar la fluctuación en los índices de precios mediante una regulación dispersa para mantener la estabilidad de todo el sistema.

Figura 5
El k-núcleo en la estructura de redes de correlación del índice de precios.
La clase de agrupamiento de grupo es mostrado en la Tabla S2.


Figura 6
Un archivo externo que contiene una imagen, ilustración, etc.

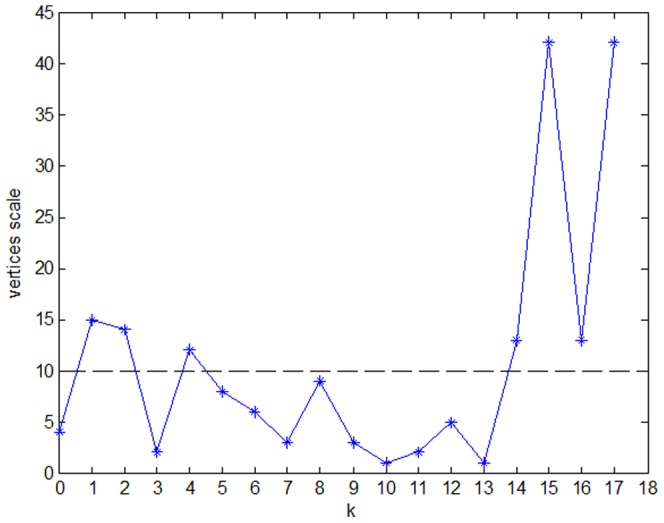La escala de vértices k-núcleo en la estructura de la red de correlación de índices de precios.

Posteriormente, el método k-plex se utiliza para buscar clusters de grupo en el PIWN bajo las condiciones más exigentes ajustando el valor de k y la escala de vértices. En el experimento, ponemos la escala de vértices a g = 17 y el coeficiente de ajuste a k = 2, y solo se encuentran 2 grupos de grupos. Los grupos de 2 grupos son colecciones de índices de precios que tienen las correlaciones más estrechas en toda la estructura de la red, como se muestra en la Figura 7. Los vértices rojos y los vértices azules representan dos grupos de racimos y los vértices negros son los índices comunes de precios para estos dos grupos de grupos . Como se observa en la Figura 7, los índices comunes de precios son todos los índices de precios macroeconómicos que se componen del IPC, el IPR y el API. De los elementos constitutivos de los 2 grupos de grupos, podemos encontrar que, en el PIWN, hay 2 grupos de grupos con estrechas correlaciones; Un grupo comprende los índices de precios de los alimentos y el otro grupo comprende los índices de precios de los bienes de consumo del PPI. Estos dos grupos de clusters tienen fuertes relaciones positivas con los índices de precios macro, lo que significa que es eficaz para China para regular y estabilizar los mercados de precios a través de los alimentos y los índices de precios aguas arriba en la red.

Figura 7
Agrupamientos de grupos de precios.

g = 17, k = 2.

Medio de transmisión

Cuando cambia uno de los índices de precios, ¿cuáles son los índices de precios que transmitirán el impacto de la fluctuación? Para responder a esta pregunta, debemos analizar el intermediario de cada índice de precios en el PIWN. En los sistemas económicos, la fluctuación de cualquier precio de las materias primas puede causar cambios en los precios de otras materias primas, y esta fluctuación es transitiva. Este efecto de transmisión se basa en las correlaciones entre los precios de los productos básicos. Al igual que controlar la propagación de un virus, no sólo debemos controlar la fuente del virus sino también detener la transmisión eliminando el medio de masa. En un sistema económico, el índice de precios en la estructura de la red actúa no sólo como fuente y receptor del proceso de transmisión sino también como medio. Diferentes índices de precios tienen diferentes niveles de efectos medios. Podríamos controlar la transmisión de fluctuaciones entre índices de precios mediante el control de los medios, para evitar la influencia de todo el sistema.

Para buscar el índice de precios que desempeña el papel de intermediario, debemos analizar la jerarquía de los agujeros estructurales para cada índice de precios en el PIWN. La presencia de agujeros estructurales hace que el índice de precios que ocupa la posición intermedia sea un enlace importante. Los agujeros estructurales controlan en gran medida la transferencia de fluctuaciones en el índice de precios. Al medir el nivel de los agujeros estructurales y calcular la jerarquía de los agujeros estructurales para cada índice de precios en la estructura de la red, una jerarquía más alta significa que el índice de precios es más importante en el proceso de transferencia. La formulación de índices de precios i en el cálculo de la jerarquía de estructuras de red es

          (6)

Donde N es el número de vértices en la red individual de vértices (índice de precios) i,  C/N es el valor medio de la restricción en cada nodo y la restricción de nodos Cij es el grado en que los nodos de la red tienen la capacidad de uso de huecos estructurales. La ecuación relevante puede expresarse como

         (7)
Donde  piq es la parte de las relaciones de los vértices j en comparación con todas las relaciones de los vértices i.

Mediante el cálculo de la jerarquía de los agujeros estructurales de cada índice de precios (véase el cuadro S3), la jerarquía de los agujeros estructurales de los índices de precios con un grado de influencia no inferior a 10 (grado ponderado> = 10) Los principales índices de precios son índices de tipo PPI, lo que significa que, en el PIWN, el PPI tiene fuertes efectos de transmisión; Sin embargo, los índices de precios de los alimentos y los medios impresos en el índice de precios al productor tienen efectos de transmisión más fuertes, con un grado de influencia de más de 25. Por lo tanto, para moderar la fluctuación de los índices de precios de los productos básicos es importante regular y controlar estos precios Con fuertes efectos de transmisión. Los resultados del experimento muestran que los índices de precios con una jerarquía de agujeros estructurales de más de 0,02 tienen un grado de influencia inferior a 8. Estos resultados muestran que, aunque algunos índices de precios en la estructura de la red tienen un pequeño grado de influencia, Desempeñan un papel importante en la transmisión de las fluctuaciones de los precios. Al mismo tiempo, encontramos que las fluctuaciones de precios entre grupos de clusters se llevan a cabo por sus índices de precios mutuos. Como se muestra en la Figura 6, los nodos negros son medios conductores de 2 grupos de grupos.

Tabla 4

Jerarquía de los hoyos estructurales de los indices de precios con un grado de influencia no menor a 10 (top 10 de los indices de precios).

Rango	Tipo de índice de precios	Grado ponderado	Jerarquía
1	CPI(Touring and Outing)	13.05	0.01843
2	PPI(Processing of Food from Agricultural Products)	28.77	0.01412
3	PPI(Food)	32.70	0.01405
4	PPI(Printing, Reproduction of Recording Media)	27.84	0.01378
5	RPI(Furniture)	27.79	0.01312
6	PPI(Food Industry)	30.13	0.01269
7	CPI(Intercity Traffic Fare)	11.43	0.01253
8	CPI(Transportation)	11.38	0.01253
9	API	36.18	0.01242
10	PPI(Raw Materials Industry)	26.43	0.01236

Distancia de transmisión y trayectoria

Cuando uno de los índices de precios cambia, hasta dónde puede llegar el proceso de transmisión, y cuál es el camino de transmisión? Para responder a esta pregunta, debemos conocer la distancia de transmisión más corta entre los índices de precios. La distancia de transmisión más corta en el PIWN se puede determinar calculando el trayecto más corto. Esta distancia se puede definir como el número mínimo de bordes a través del cual pasan los dos índices de precios en la estructura de la red. Cuando un índice de precios cambia, podemos medir la distancia de impacto más larga calculando el trayecto más corto entre este índice de precios y otros. Además, podríamos conocer la distancia de impacto de todo el sistema de índices de precios al encontrar la trayectoria media más corta del PIWN. Por lo tanto, cuando un índice de precios cambia, podríamos saber qué índice de precios se verá afectado a continuación.

Como se muestra en la Figura 8, las distancias de transmisión de los índices de precios siguen una distribución normal. Una distancia de 1 significa que los dos índices de precios en el PIWN están conectados directamente. Los cambios en cualquiera de los índices de precios afectarán al otro. Se considera que la distancia de impacto es 1. Una distancia de 2 significa que los dos índices de precios están conectados por otro índice de precios (conectado indirectamente). Así, la distancia de impacto se expande a 2. Después de continuar de esta manera, la Figura 8 muestra que las distancias de transmisión de los índices de precios se concentran entre 2 y 4. Así, generalmente las distancias de transmisión de la mayoría de los índices de precios son 2-4 , Lo que significa que, cuando un índice de precios cambia, sólo 2-4 distancias son necesarias para afectar a la mayoría. La distancia de transmisión de fluctuación más larga es de 9 en el PIWN, lo que significa que, cuando cambia un determinado índice de precios, el sistema de índice de precios se verá afectado a una distancia de 9. La longitud de trayecto más corta promedio es 2,55. El índice de cohesión de la estructura de red basado en "distancia" es 0.953. Por lo tanto, la transmisión entre los índices de precios en la estructura de la red es relativamente rápida, tiene un efecto de pequeño mundo, y, en promedio, puede ser completado por un índice de precios. Los resultados también muestran que, en la inflación real, un vértice a menudo tiene un impacto en todos los precios de las materias primas antes de tomar medidas de control efectivas.

Figura 8
Distancia más corta y frecuencia entre los índices de precios.

Después de una distribución normal con un nivel de confianza de 0,78.

Analizamos los caminos en el PIWN y encontramos la trayectoria de transmisión basada en los pesos de los bordes. Tomando el IPR como ejemplo (el valor de su grado ponderado es el más grande), cuando el IPR cambia, el nodo más correlacionado es CPI, y el nodo más correlacionado con IPC es IPC (Hogar Urbano). Siguiendo este proceso, podríamos encontrar otros nodos. De acuerdo con el camino más corto que hemos obtenido anteriormente, la distancia de transmisión más larga es 9; Como resultado, cuando encontramos el 10mo nodo, el RPI (Casa Rural) ya había afectado a todo el sistema. La trayectoria de transmisión del RPI (Casa Rural) se muestra en la Figura 9, con las correlaciones entre los índices de precios (pesos de los bordes) por encima de 0.96. Por supuesto, sólo habíamos considerado el camino con las correlaciones más fuertes. En realidad, los nodos de la trayectoria de transmisión pasarán la fluctuación a otros nodos. Podríamos utilizar el mismo método para encontrar todos los caminos de transmisión y luego conocer más completamente el proceso de transmisión de los índices de precios.

Figura 9

Senderos de transmisión de RPI (Rural Household) con las correlaciones más fuertes.

Discusiones y conclusiones

Este artículo analiza las características de la estructura de correlación de los índices de precios por los métodos que implican redes complejas. Teóricamente, consideramos las relaciones entre muchos factores y realizamos la investigación con una visión estructurada, mientras que la econometría tradicional sólo puede analizar las relaciones entre algunos factores. En la práctica, este enfoque podría ayudarnos a conocer más sobre las interacciones de los índices de precios analizando las características de la estructura de correlación. Este análisis no sólo nos muestra los principios de las interacciones de los índices de precios en el sistema económico sino que también nos proporciona pruebas efectivas de las políticas de control macroeconómico para el gobierno. Encontrar los índices clave de precios podría hacernos conscientes de qué objeto de control es el objetivo clave; El análisis de los grupos de grupos podría mostrarnos las influencias entre los índices de precios, y luego, podríamos sugerir al gobierno cómo estabilizar el precio de mercado regulando escasamente. Analizar el medio de transmisión nos muestra el nivel medio de cada índice de precios, y el gobierno podría evitar la expansión de las fluctuaciones mediante el control de los medios. Medir la distancia de transmisión y descubrir el camino nos indica la escala de impacto y su trayectoria de transmisión cuando hay fluctuaciones en los índices de precios; Estas rutas de transmisión proporcionan referencias cuando se hacen políticas de advertencia.

Un tema que debe investigarse más es cómo estudiar las relaciones que involucran muchas variables si el número de factores que afectan en un sistema económico continúa aumentando; Hay cientos o incluso miles de factores que interactúan entre sí. Como se muestra en la revisión bibliográfica, la mayoría de los estudios sobre la relación entre variables usan teorías y métodos de econometría como regresiones lineales, pruebas de causalidad y pruebas de cointegración. Sin embargo, el propósito de estos modelos econométricos no es incluir todas las variables; En cambio, el propósito es incluir sólo los factores más significativos. Si se introducen demasiadas variables, entonces el modelo será demasiado complejo y la investigación perderá sentido. El número de objetos incluidos en los métodos econométricos tradicionales es dos; Incluso si hay múltiples variables, el análisis se realiza con sólo dos variables. Además, muchos de los objetos incluidos son macroscópicos. Por lo tanto, es fácil ignorar las variables de nivel micro. Estas variables tienen correlaciones e influencia, e interactúan entre sí para formar un complicado sistema de relaciones. Los cambios macroscópicos son causados ​​por cambios en la complejidad de estas variables. Las investigaciones existentes rara vez abordan estas cuestiones. La teoría de red compleja proporciona una buena base para abordar el problema de la complejidad. Las relaciones entre las variables se resumen en los vértices y los bordes de la red, aplicando la investigación sobre la relación entre las numerosas variables en la red. El complejo método de análisis de red proporciona una gama de parámetros y puede combinarse con teorías económicas y métodos analíticos para estudiar problemas complejos en el sistema de índices de precios y el sistema financiero e incluso en el sistema económico.

Al construir el modelo de estructura de la red de correlación de índices de precios, el método no sólo puede utilizarse para estudiar la estructura de correlación de los índices de precios, sino también para otros campos, como el análisis de la correlación entre diversos elementos de los mercados de productos básicos, De los vínculos de precios de las acciones en los mercados financieros, de la investigación sobre las relaciones insumo-producto en las cadenas industriales y de la investigación sobre las relaciones de correlación entre los diversos índices económicos nacionales. Estas cuestiones involucran más variables y relaciones más complejas. Otras investigaciones deberían tener como objetivo definir relaciones complejas entre más variables y combinar métodos de análisis cualitativos y cuantitativos.

Referencias

1. Lebow DE, Rudd JB (2006) Inflation measurement. Finance and economics discussion series divisions of research & statistics and monetary affairs. Federal Reserve Board, Washington, D.C. 1–17
2. Alchian AA, Klein B (1973) On a correct measure of inflation. Journal of Money, Credit and Banking 5: 173–191
3. Mankiw NG, Reis R (2003) What measure of infaltion should a central bank target?. Journal of the European Economic Association 1: 1058–1086
4. Silver JL, Wallace D (1980) The lag relationship between wholesale and consumer prices. Journal of Econometrics 12: 375–387
5. Mahdavi S, Zhou S (1997) Gold and commodity prices as leading indicators of inflation: tests of long-run relationship and predictive performance. Journal of Economics and Business 49: 475–489
6. Kyrtsou C, Labys W (2006) Evidence for chaotic dependence between US inflation and commodity prices. Journal of Macroeconomics 28: 256–266
7. Blomberg SB, Harris ES (1995) The commodity-consumer price connection: fact or fable?. Economic Policy Review 1: 21–38
8. Doroodian K, Boyd R (2003) The linkage between oil price shocks and economic growth with inflation in the presence of technological advances: a CGE model. Energy Policy 31: 989–1006
9. Johnson GD, Song G (1998) Inflation and the Real Price of Grain in China. Chinese Economies Research Center, Working Paper, University of Adelaide.
10. Kadeřábek P (2007) A simple model of interaction between CPI and PPI: Application to monthly data of EU countries. Politická ekonomie 55: 226–244
11. Cushing MJ (1990) Freedback between Whosale and Consumer Price Inflation: A reexamination of the evidence. Southern Economic Journal 56: 1059–1072
12. Clark TE (1995) Do producer prices lead consumer prices?. Economic Review QIII 25–39
13. Weinhagen J (2005) Price transmission within the PPI for intermediate goods. Monthly Labor Review 5: 41–49
14. Gujarati DN, Porter DC (2010) Essentials of Econometrics, 4th edition. McGraw Hill Higher Education.
15. Peazzo RPJ, Reich SL, Schvarzer J, Virasoro MA (1995) Inflation and relaxation to equilibrium in a complex economic-system. Chaos Solitions & Fractals 6: 455–470
16. Schweitzer F, Fagiolo G, Sornette D, Vega-Redondo F, Vespignani A, et al. (2009) Economic Networks: The New Challenges. Science 325: 422–425 [PubMed]
17. Elgazzar AS (2003) Applications of small-world networks to some socio-economic systems. Physica A: Statistical Mechanics and its Applications 324: 402–407
18. Watts DJ, Strogatz SH (1998) Collective dynamics of ‘small-world’ networks. Nature 393: 440–442 [PubMed]
19. Newman MEJ, Watts DJ (1999) Renormalization group analysis of the small-world network model. Physics Letters A 263: 341–346
20. Barabási AL, Albert R (1999) Emergence of Scaling in Random Networks. Science 286: 509–512 [PubMed]
21. Latora V, Marchiori M (2003) Economic small-world behavior in weighted networks. The European Physical Journal B 32: 249–263
22. Eagle N, Macy M, Claxton R (2010) Network Diversity and Economic Development. Science 328: 1029–1031 [PubMed]
23. Liu XF, Tse CK (2012) A complex network perspective of world stock markets : synchronization and volatility. International Journal of Bifurcation and Chaos 22: 1250142
24. Kenett DY, Tumminello M, Madi A, Gur-Gershgoren G, Mantegna RN, et al. (2010) Dominating clasp of the financial sector revealed by partial correlation analysis of the stock market. PLoS ONE 5: e15032. [PMC free article] [PubMed]
25. Tse CK, Liu J, Lau FC (2010) A network perspective of the stock market. Journal of Empirical Finance 17: 659–667
26. He LP, Liu QW (2011) Causes of Inflation in China: Inflation Expectations. China & World Economy 19: 18–32