Este blog reúne material del curso de posgrado "Análisis de redes sociales" dictado en la Universidad Nacional del Sur (Argentina).
martes, 12 de noviembre de 2013
domingo, 10 de noviembre de 2013
ARS 101: Centralidad, componentes y otros temas de redes
Lada Adamic nos comenta sobre centralidad y componentes conectados
Lada Adamic, ganadora en 2012 del afamado premio Henry Russell, es una científica social experta en redes sociales de la Universidad de Michigan. En esta exposición introductoria comenta sobre centralidad y componentes conectados. Los subtítulos en español y sus errores son responsabilidad mía.
Lada Adamic, ganadora en 2012 del afamado premio Henry Russell, es una científica social experta en redes sociales de la Universidad de Michigan. En esta exposición introductoria comenta sobre centralidad y componentes conectados. Los subtítulos en español y sus errores son responsabilidad mía.
sábado, 9 de noviembre de 2013
viernes, 8 de noviembre de 2013
ARS 101: Modularidad
Modularidad en redes
La modularidad es una medida de la estructura de las redes o grafos. Fue diseñado para medir la fuerza de la división de una red en módulos (también llamados grupos, agrupamientos o comunidades). Las redes con alta modularidad tienen conexiones sólidas entre los nodos dentro de los módulos, pero escasas conexiones entre nodos en diferentes módulos. La modularidad se utiliza a menudo en los métodos de optimización para la detección de la estructura comunitaria de las redes. Sin embargo, se ha demostrado que la modularidad sufre un límite de resolución y, por lo tanto, no es capaz de detectar pequeñas comunidades. Las redes biológicas, incluidos los cerebros animales, presentan un alto grado de modularidad.
Existen diferentes métodos para el cálculo de la modularidad. [1] En la versión más común del concepto, la aleatorización de los enlaces se realiza con el fin de preservar el grado de cada vértice. Veamos un grafo con nodos y
nodos y  enlaces (enlaces) de tal manera que el grafo se puede dividir en 2 comunidades usando una variable de membrecía
enlaces (enlaces) de tal manera que el grafo se puede dividir en 2 comunidades usando una variable de membrecía  Si un nodo
Si un nodo  pertenece a la comunidad 1,
pertenece a la comunidad 1, 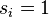 o si
o si  pertenece a la comunidad 2,
pertenece a la comunidad 2,  Sea que la matriz de adyacencia de la red estará representado por A, donde
Sea que la matriz de adyacencia de la red estará representado por A, donde 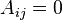 significa que no hay ninguna ventaja (sin interacción) entre los nodos i y j y
significa que no hay ninguna ventaja (sin interacción) entre los nodos i y j y 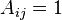 significa que hay un enlace entre los dos. También por simplicidad consideramos una red no dirigida. Así
significa que hay un enlace entre los dos. También por simplicidad consideramos una red no dirigida. Así  (Es importante tener en cuenta que pueden existir múltiples enlaces entre los nodos 2 y aquí evaluamos el caso más simple).
(Es importante tener en cuenta que pueden existir múltiples enlaces entre los nodos 2 y aquí evaluamos el caso más simple).
La modularidad Q se define entonces como la fracción de enlaces que caen dentro del grupo 1 o 2, menos el número esperado de enlaces dentro del grupo 1 y 2 para un grafo aleatorio con el mismo grado de distribución como el nodo de red determinado.
El número esperado de enlaces se calcula utilizando el concepto de modelos de configuración. [3] El modelo de configuración es una realización aleatoria de una red en particular. Dada una red con n nodos, donde cada nodo i tiene un grado nodal , el modelo de configuración corta cada enlace en 2 mitades, y luego cada media punta, llamados a trozo, es reconectado al azar con cualquier otro ramal en la red, incluso permitiendo auto bucles. Por lo tanto, a pesar de que la distribución de grado de nodo del grafo permanece intacta, los resultados del modelo de configuración en una red completamente al azar.
, el modelo de configuración corta cada enlace en 2 mitades, y luego cada media punta, llamados a trozo, es reconectado al azar con cualquier otro ramal en la red, incluso permitiendo auto bucles. Por lo tanto, a pesar de que la distribución de grado de nodo del grafo permanece intacta, los resultados del modelo de configuración en una red completamente al azar.

Ahora, si se selecciona al azar dos nodos i y j con grados nodo ki y kj respectivamente, y recablear los ramales a estos 2 nodos y, a continuación,
Número esperado de enlaces [enlaces completos entre i y j] = (enlaces completos entre i y j) / (número total de posibles reconexiones) (2)
Número total de reconexiones posibles = número de ramales que quedan después de la elección de un determinado ramal = ln- 1 = ln para n grande
Por lo tanto, se esperaba [Número de enlaces completos entre i y j] = (ki * kJ) / ln = (ki kJ) / 2m.
Por lo tanto, el número real de enlaces entre i y j menos el número esperado de enlaces entre ellos es Aij - (ki kj) / 2 m. Por lo tanto el uso de [1]
![Q = \frac{1}{2m} \sum_{ij} \left[ A_{ij} - \frac{k_i*k_j}{2m} \right] \frac{s_{i} s_{j}+1}{2} (3)](http://upload.wikimedia.org/math/0/c/e/0ce69089d0d0d539bf98fb475625e45b.png)
Es importante tener en cuenta que (3) es válido para la partición en sólo 2 comunidades. La partición jerárquica (es decir, partición en 2 comunidades, a continuación, las 2 sub- comunidades con particiones más en 2 comunidades más pequeñas sub sólo para maximizar Q) es un posible enfoque para identificar múltiples comunidades en una red. Además, (3) puede ser generalizada para la partición de una red en comunidades c. [4]
![Q = \sum_{ij} \left[ \frac {A_{ij}}{2m} - \frac{k_i*k_j}{(2m)(2m)} \right] \delta(c_{i}, c_{j})
=\sum_{i=1}^{c} (e_{ii}-a_{i}^2) (4)](http://upload.wikimedia.org/math/d/9/2/d92fbe96f23717f14456b6b40389a2a7.png)
eii donde es la fracción de los enlaces con ambas vértices finales de la misma comunidad i:

y ai es la fracción de enlaces con al menos un extremo de vértice en la comunidad i :

Consideramos una red no dirigida con 10 nodos y 12 enlaces y la siguiente matriz de adyacencia.
 Fig. 1. Red de muestra correspondiente a la matriz de adyacencia con 10 nodos, 12 enlaces.
Fig. 1. Red de muestra correspondiente a la matriz de adyacencia con 10 nodos, 12 enlaces.
 Fig. 2. Particiones de red que maximizan Q. máxima Q = 0.4895
Fig. 2. Particiones de red que maximizan Q. máxima Q = 0.4895
Las comunidades en la gráfica están representados por los grupos de nodos de color rojo, verde y azul en la figura 1. Las particiones de la comunidad óptimos se representan en la figura 2.

y por lo tanto
![Q = \frac{1}{2m} \sum_{ij} \sum_r \left[ A_{ij} - \frac{k_i k_j}{2m} \right] S_{ir} S_{jr}
= \frac{1}{2m} \mathrm{Tr}(\mathbf{S}^\mathrm{T}\mathbf{BS}),](http://upload.wikimedia.org/math/1/d/8/1d820355e27e66d2d0f14f3efa0248a9.png)
donde S es teniendo la matriz (no cuadrados) elementos Sir y B es la llamada matriz de modularidad, que tiene elementos

Todas las filas y columnas de la matriz de modularidad suma a cero, lo que significa que la modularidad de una red indivisa también es siempre cero.
Para redes divididas en sólo dos comunidades, se puede definir como alternativa si = ± 1 para indicar que la comunidad a la que pertenece el nodo i, que a su vez conduce a
 ,
,
donde s es el vector columna con elementos de SI. [1]
Esta función tiene la misma forma que el hamiltoniano de un vidrio de espín Ising, una conexión que ha sido explotada para crear algoritmos computacionales simples, por ejemplo mediante el recocido simulado, para maximizar la modularidad. La forma general de la modularidad para un número arbitrario de las comunidades es equivalente a un vidrio de espín Potts y algoritmos similares puede ser desarrollado para este caso también. [5]
La modularidad es una medida de la estructura de las redes o grafos. Fue diseñado para medir la fuerza de la división de una red en módulos (también llamados grupos, agrupamientos o comunidades). Las redes con alta modularidad tienen conexiones sólidas entre los nodos dentro de los módulos, pero escasas conexiones entre nodos en diferentes módulos. La modularidad se utiliza a menudo en los métodos de optimización para la detección de la estructura comunitaria de las redes. Sin embargo, se ha demostrado que la modularidad sufre un límite de resolución y, por lo tanto, no es capaz de detectar pequeñas comunidades. Las redes biológicas, incluidos los cerebros animales, presentan un alto grado de modularidad.
Motivación
Muchos problemas científicamente importantes se pueden representar y ser empíricamente estudiados a través de redes. Por ejemplo, los patrones biológicos y sociales, la World Wide Web, las redes metabólicas, redes tróficas, redes neuronales y redes patológicos son algunos ejemplos de los problemas del mundo real que pueden ser representados matemáticamente y topológicamente estudiaron para revelar algunas características estructurales inesperadas. [1] La mayoría de estas redes poseen una cierta estructura de comunidad que tiene considerable importancia en la construcción de un entendimiento respecto a la dinámica de la red. Por ejemplo, una comunidad social estrechamente relacionado implicará una mayor velocidad de transmisión de información o rumor entre ellos de una comunidad mal conectados. Por lo tanto, si una red está representado por un número de nodos individuales conectadas por enlaces que significan un cierto grado de interacción entre los nodos, las comunidades se definen como grupos de nodos densamente interconectados que son sólo escasamente conectados con el resto de la red. Por lo tanto, puede ser imprescindible identificar comunidades en las redes ya que las comunidades pueden tener propiedades muy diferentes, tales como grado, coeficiente de agrupamiento, intermediación, centralidad nodal [2], etc, respecto a la media de la red. La modularidad es una de tales medidas, que, cuando se maximiza, sino que conduce a la aparición de comunidades en una red dada.Definición
La modularidad es la fracción de los enlaces que caen dentro de grupos dados menos el valor esperado que dicha fracción hubiese recibido si los enlaces se hubiesen distribuido al azar. El valor de la modularidad se encuentra en el intervalo [-.5,1). Es positivo si el número de enlaces dentro de los grupos supera el número esperado sobre la base de pura casualidad. Para una determinada división de vértices de la red en algunos módulos, la modularidad refleja la concentración de los nodos dentro de los módulos en comparación con distribución al azar de los enlaces entre todos los nodos, independientemente de los módulos.Existen diferentes métodos para el cálculo de la modularidad. [1] En la versión más común del concepto, la aleatorización de los enlaces se realiza con el fin de preservar el grado de cada vértice. Veamos un grafo con
 nodos y
nodos y  enlaces (enlaces) de tal manera que el grafo se puede dividir en 2 comunidades usando una variable de membrecía
enlaces (enlaces) de tal manera que el grafo se puede dividir en 2 comunidades usando una variable de membrecía  Si un nodo
Si un nodo  pertenece a la comunidad 1,
pertenece a la comunidad 1, 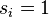 o si
o si  pertenece a la comunidad 2,
pertenece a la comunidad 2,  Sea que la matriz de adyacencia de la red estará representado por A, donde
Sea que la matriz de adyacencia de la red estará representado por A, donde 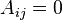 significa que no hay ninguna ventaja (sin interacción) entre los nodos i y j y
significa que no hay ninguna ventaja (sin interacción) entre los nodos i y j y 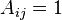 significa que hay un enlace entre los dos. También por simplicidad consideramos una red no dirigida. Así
significa que hay un enlace entre los dos. También por simplicidad consideramos una red no dirigida. Así  (Es importante tener en cuenta que pueden existir múltiples enlaces entre los nodos 2 y aquí evaluamos el caso más simple).
(Es importante tener en cuenta que pueden existir múltiples enlaces entre los nodos 2 y aquí evaluamos el caso más simple).La modularidad Q se define entonces como la fracción de enlaces que caen dentro del grupo 1 o 2, menos el número esperado de enlaces dentro del grupo 1 y 2 para un grafo aleatorio con el mismo grado de distribución como el nodo de red determinado.
El número esperado de enlaces se calcula utilizando el concepto de modelos de configuración. [3] El modelo de configuración es una realización aleatoria de una red en particular. Dada una red con n nodos, donde cada nodo i tiene un grado nodal
 , el modelo de configuración corta cada enlace en 2 mitades, y luego cada media punta, llamados a trozo, es reconectado al azar con cualquier otro ramal en la red, incluso permitiendo auto bucles. Por lo tanto, a pesar de que la distribución de grado de nodo del grafo permanece intacta, los resultados del modelo de configuración en una red completamente al azar.
, el modelo de configuración corta cada enlace en 2 mitades, y luego cada media punta, llamados a trozo, es reconectado al azar con cualquier otro ramal en la red, incluso permitiendo auto bucles. Por lo tanto, a pesar de que la distribución de grado de nodo del grafo permanece intacta, los resultados del modelo de configuración en una red completamente al azar.Número esperado de enlaces entre nodos
Si el número total de ramales es ln
Ahora, si se selecciona al azar dos nodos i y j con grados nodo ki y kj respectivamente, y recablear los ramales a estos 2 nodos y, a continuación,
Número esperado de enlaces [enlaces completos entre i y j] = (enlaces completos entre i y j) / (número total de posibles reconexiones) (2)
Número total de reconexiones posibles = número de ramales que quedan después de la elección de un determinado ramal = ln- 1 = ln para n grande
Por lo tanto, se esperaba [Número de enlaces completos entre i y j] = (ki * kJ) / ln = (ki kJ) / 2m.
Por lo tanto, el número real de enlaces entre i y j menos el número esperado de enlaces entre ellos es Aij - (ki kj) / 2 m. Por lo tanto el uso de [1]
![Q = \frac{1}{2m} \sum_{ij} \left[ A_{ij} - \frac{k_i*k_j}{2m} \right] \frac{s_{i} s_{j}+1}{2} (3)](http://upload.wikimedia.org/math/0/c/e/0ce69089d0d0d539bf98fb475625e45b.png)
Es importante tener en cuenta que (3) es válido para la partición en sólo 2 comunidades. La partición jerárquica (es decir, partición en 2 comunidades, a continuación, las 2 sub- comunidades con particiones más en 2 comunidades más pequeñas sub sólo para maximizar Q) es un posible enfoque para identificar múltiples comunidades en una red. Además, (3) puede ser generalizada para la partición de una red en comunidades c. [4]
![Q = \sum_{ij} \left[ \frac {A_{ij}}{2m} - \frac{k_i*k_j}{(2m)(2m)} \right] \delta(c_{i}, c_{j})
=\sum_{i=1}^{c} (e_{ii}-a_{i}^2) (4)](http://upload.wikimedia.org/math/d/9/2/d92fbe96f23717f14456b6b40389a2a7.png)
eii donde es la fracción de los enlaces con ambas vértices finales de la misma comunidad i:

y ai es la fracción de enlaces con al menos un extremo de vértice en la comunidad i :

Ejemplo de detección múltiple comunidad
Consideramos una red no dirigida con 10 nodos y 12 enlaces y la siguiente matriz de adyacencia.
 Fig. 1. Red de muestra correspondiente a la matriz de adyacencia con 10 nodos, 12 enlaces.
Fig. 1. Red de muestra correspondiente a la matriz de adyacencia con 10 nodos, 12 enlaces. Fig. 2. Particiones de red que maximizan Q. máxima Q = 0.4895
Fig. 2. Particiones de red que maximizan Q. máxima Q = 0.4895| Nodo ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 5 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Formulación matricial
Una formulación alternativa de la modularidad, útil en particular en algoritmos de optimización espectrales, es como sigue. [1] Definir Sir sea 1 si vértice i pertenece al grupo de r y cero en caso contrario. entonces
y por lo tanto
![Q = \frac{1}{2m} \sum_{ij} \sum_r \left[ A_{ij} - \frac{k_i k_j}{2m} \right] S_{ir} S_{jr}
= \frac{1}{2m} \mathrm{Tr}(\mathbf{S}^\mathrm{T}\mathbf{BS}),](http://upload.wikimedia.org/math/1/d/8/1d820355e27e66d2d0f14f3efa0248a9.png)
donde S es teniendo la matriz (no cuadrados) elementos Sir y B es la llamada matriz de modularidad, que tiene elementos

Todas las filas y columnas de la matriz de modularidad suma a cero, lo que significa que la modularidad de una red indivisa también es siempre cero.
Para redes divididas en sólo dos comunidades, se puede definir como alternativa si = ± 1 para indicar que la comunidad a la que pertenece el nodo i, que a su vez conduce a
 ,
,donde s es el vector columna con elementos de SI. [1]
Esta función tiene la misma forma que el hamiltoniano de un vidrio de espín Ising, una conexión que ha sido explotada para crear algoritmos computacionales simples, por ejemplo mediante el recocido simulado, para maximizar la modularidad. La forma general de la modularidad para un número arbitrario de las comunidades es equivalente a un vidrio de espín Potts y algoritmos similares puede ser desarrollado para este caso también. [5]
Límite de resolución
La modularidad compara el número de enlaces dentro de un grupo con el número esperado de enlaces que uno encontraría en el grupo si la red fuera una red aleatoria con el mismo número de nodos y donde cada nodo mantiene su grado, pero los enlaces son lo contrario adjunta al azar. Este modelo nulo al azar asume implícitamente que cada nodo puede quedar unido a cualquier otro nodo de la red. Tal suposición es razonable sin embargo si la red es muy grande, como el horizonte de un nodo incluye una pequeña parte de la red, haciendo caso omiso de la mayor parte de ella. Por otra parte, esto implica que el número esperado de enlaces entre dos grupos de nodos disminuye si el tamaño de la red aumenta. Así, si una red es lo suficientemente grande, el número esperado de enlaces entre dos grupos de nodos en modelo nulo de modularidad puede ser menor que uno. Si esto sucede, un solo borde entre los dos grupos sería interpretado por la modularidad como un signo de una fuerte correlación entre los dos grupos, y la optimización de la modularidad conduciría a la fusión de los dos grupos, independientemente de las características de la agrupación. Por lo tanto, incluso débilmente interconectado gráficos completos, que tienen la densidad más alta posible de los enlaces internos, y representan las mejores comunidades identificables, se fusionara por optimización modularidad si la red es suficientemente grande. [6] Por este motivo, la optimización de la modularidad en redes grandes sería un fracaso para resolver las pequeñas comunidades, incluso cuando están bien definidos. Este sesgo es inevitable para los métodos como la optimización de la modularidad, que se basan en un modelo nulo global. [7]Métodos multirresolución
Hay dos enfoques principales que tratan de resolver el límite de resolución en el contexto modularidad : la adición de un r resistencia a todos los nodos, en la forma de un auto -loop, lo que aumenta (r> 0) o disminuye (r < 0) la aversión de los nodos a las comunidades de formulario ; [8] o la adición de un parámetro γ > 0 en frente del término nulo caso en la definición de la modularidad, que controla la importancia relativa entre los enlaces internos de las comunidades y el modelo nulo. [5] modularidad Optimización para los valores de estos parámetros en sus respectivos rangos adecuados, es posible recuperar toda la mesoescala de la red, desde la macroescala en la que todos los nodos pertenecen a la misma comunidad, a la microescala en el que cada nodo forma su propia comunidad, por lo tanto, los métodos de varias resoluciones de nombres. Sin embargo, se ha demostrado recientemente que estos métodos son intrínsecamente deficiente y su uso no producirán soluciones fiables. [9]Referencias
- Jump up to:Newman, M. E. J. (2006). "Modularity and community structure in networks". Proceedings of the National Academy of Sciences of the United States of America 103 (23): 8577–8696. arXiv:physics/0602124. Bibcode:2006PNAS..103.8577N.doi:10.1073/pnas.0601602103. PMC 1482622. PMID 16723398.
- Jump up Newman, M. E. J. (2007). "Mathematics of networks". In Palgrave Macmillan, Basingstoke. The New Palgrave Encyclopedia of Economics (2 ed.).
- Jump up Remco van der Hofstad (2009). "7". Random Graphs and Complex Networks.
- Jump upClauset, Aaron and Newman, M. E. J. and Moore, Cristopher (2004). "Finding community structure in very large networks". Phys. Rev. E 70 (6): 066111. arXiv:cond-mat/0408187. Bibcode:2004PhRvE..70f6111C. doi:10.1103/PhysRevE.70.066111.
- Joerg Reichardt and Stefan Bornholdt (2006). "Statistical mechanics of community detection". Physical Review E 74 (1): 016110. arXiv:cond-mat/0603718. Bibcode:2006PhRvE..74a6110R. doi:10.1103/PhysRevE.74.016110.
- Jump up Santo Fortunato and Marc Barthelemy (2007). "Resolution limit in community detection". Proceedings of the National Academy of Sciences of the United States of America 104 (1): 36–41. arXiv:physics/0607100. Bibcode:2007PNAS..104...36F.doi:10.1073/pnas.0605965104. PMC 1765466. PMID 17190818.
- Jump upJ.M. Kumpula, J. Saramäki, K. Kaski , and J. Kertész (2007). "Limited resolution in complex network community detection with Potts model approach". European Physical Journal B 56 (1): 41–45. arXiv:cond-mat/0610370. Bibcode:2007EPJB...56...41K.doi:10.1140/epjb/e2007-00088-4.
- Jump up Alex Arenas, Alberto Fernández and Sergio Gómez (2008). "Analysis of the structure of complex networks at different resolution levels". New Journal of Physics 10 (5): 053039. arXiv:physics/0703218. Bibcode:2008NJPh...10e3039A. doi:10.1088/1367-2630/10/5/053039.
- Jump up Andrea Lancichinetti and Santo Fortunato (2011). "Limits of modularity maximization in community detection". Physical Review E 84: 066122. arXiv:1107.1155. Bibcode:2011PhRvE..84f6122L. doi:10.1103/PhysRevE.84.066122.
jueves, 7 de noviembre de 2013
Minando Twitter con R para construir datos para análisis de sentimiento
Mining Twitter with R - Tutorial 1: Building a corpus from Twitter data
Tutorial 1 - Building a corpus from Twitter data:http://youtu.be/mJVcANlkxU8
Tutorial 2 - Scoring tweets: http://youtu.be/S1y3PxULNaQ
Tutorial 3 - Histogram (): http://youtu.be/KDYZTFLBrZk
References
Breen, J. O. (2012). Mining twitter for airline consumer sentiment. Practical Text Mining and Statistical Analysis for Non-structured Text Data Applications, 133.
Jeffrey Breen's Blog: http://jeffreybreen.wordpress.com/201...
miércoles, 6 de noviembre de 2013
La viralización de textos en los 1800s
Here’s How Memes Went Viral — In the 1800s
- BY GREG MILLER - WIRED.COM

Thicker lines indicate more content-sharing between 19th century newspapers. Image: Ryan Cordell / Infectious texts project
The story had everything — exotic locale, breathtaking engineering, Napoleon Bonaparte. No wonder the account of a lamplit flat-bottom boat journey through the Paris sewer went viral after it was published — on May 23, 1860.
At least 15 American newspapers reprinted it, exposing tens of thousands of readers to the dank wonders of the French city’s “splendid system of sewerage.”
Twitter is faster and HuffPo more sophisticated, but the parasitic dynamics of networked media were fully functional in the 19th century. For proof, look no further than the Infectious Texts project, a collaboration of humanities scholars and computer scientists.
The project expects to launch by the end of the month. When it does, researchers and the public will be able to comb through widely reprinted texts identified by mining 41,829 issues of 132 newspapers from the Library of Congress. While this first stage focuses on texts from before the Civil War, the project eventually will include the later 19th century and expand to include magazines and other publications, says Ryan Cordell, an assistant professor of English at Northeastern University and a leader of the project.
Some of the stories were printed in 50 or more newspapers, each with thousands to tens of thousands of subscribers. The most popular of them most likely were read by hundreds of thousands of people, Cordell says. Most have been completely forgotten. “Almost none of those are texts that scholars have studied, or even knew existed,” he said.
Yellow dots represent hotspots of recycled content. The shading indicates the number of publications in a region recorded by the 1840 census. Image: Ryan Cordell / Infectious texts project
The tech may have been less sophisticated, but some barriers to virality were low in the 1800s. Before modern copyright laws there were no legal or even cultural barriers to borrowing content, Cordell says. Newspapers borrowed freely. Large papers often had an “exchange editor” whose job it was to read through other papers and clip out interesting pieces. “They were sort of like BuzzFeed employees,” Cordell said.
Clips got sorted into drawers according to length; when the paper needed, say, a 3-inch piece to fill a gap, they’d pluck out a story of the appropriate length and publish it, often verbatim.
Fast forward a century and a half and many of these newspapers have been scanned and digitized. Northeastern computer scientist David Smith developed an algorithm that mines this vast trove of text for reprinted items by hunting for clusters of five words that appear in the same sequence in multiple publications (Google uses a similar concept for its Ngram viewer).
The project is sponsored by the NULab for Texts, Maps, and Networks at Northeastern and the Office of Digital Humanities at the National Endowment for the Humanities. Cordell says the main goal is to build a resource for other scholars, but he’s already capitalizing on it for his own research, using modern mapping and network analysis tools to explore how things went viral back then.
Counting page views from two centuries ago is anything but an exact science, but Cordell has used Census records to estimate how many people were living within a certain distance of where a particular piece was published and combined that with newspaper circulation data to estimate what fraction of the population would have seen it (a quarter to a third, for the most infectious texts, he says).
He’s also interested in mapping how the growth of the transcontinental railroad — and later the telegraph and wire services — changed the way information moved across the country. The animation below shows the spread of a single viral text, a poem by the Scottish poet Charles MacKay, overlaid on the developing railroad system. The one at the very bottom depicts how newspapers grew with the country from the colonial era to modern times, often expanding into a territory before the political boundaries had been drawn.
Another approach takes advantage of the same type of network analysis tools social scientists use to map the flow of information in Twitter and other social media. Cordell has found that certain cities that don’t get much attention from scholars were actually important hubs in the 19th century information economy. Nashville is one of them. “It makes sense if you think about it,” Cordell said. “It was the center of the country at the time.”
Some of the texts that went viral in the 1800s aren’t all that different from the things people post on Facebook today, Cordell says. Political rants were popular, for example, as were recipes and travel stories.
Poems also turn up frequently, as well as another type of writing Cordell calls vignettes. These are sentimental stories that are presented as if they’re real, but aren’t attributable to an author and lack details that would make it possible to verify them. One example is a letter, supposedly tucked into a book by a dying woman and found by her husband after her death. She urges him to remember her fondly and live a good life after she’s gone. “These are fascinating to me because they blur the line between fact and fiction, which sort of exemplifies the 19th century newspaper,” Cordell said.
The vignettes often had a moral to them. On popular variety, temperance stories, were aimed at getting drunks to sober up. Cordell likens these cautionary tales to the email you’ve probably gotten from a concerned aunt or uncle that turns out to be based on a bogus urban legend when you look it up on Snopes.
The media may have changed, but a century and a half later many of the messages are surprisingly familiar.
martes, 5 de noviembre de 2013
ARS ayuda al marketing digital
How network analysis can make us better digital marketers
by Andrew Lamb

A network map of 3,930 Twitter users talking about and sharing Econsultancy links over an eight day period in October 2013

A detail of the network map of 3,930 users sharing Econsultancy.com content on Twitter
by Andrew Lamb
Social ‘networks’, computer ‘networks’, ‘networking’ events, agency ‘networks’ – even the ‘Internet’. ‘Networks’ of one form or another are everywhere, but what do all these things have in common? And how can an understanding of networks help us become better digital marketers?
I want to go beyond our often unthinking use of the word network, and explore how a deeper understanding of networkscan help us identify influencers and communities online, creating content that really resonates and is more likely to be shared.
I’ll use an example of a network generated from Twitter, showing the follow relationships between people talking about Econsultancy, and sharing links from the site, over an eight day period in October 2013.

A network map of 3,930 Twitter users talking about and sharing Econsultancy links over an eight day period in October 2013
What is a 'network'?
At its most basic, a network can be defined as a collection of ‘nodes’ (things like people, products, or web pages) connected by relationships or associations of some kind (known as ‘edges’).
Mathematicians have been wrestling with networks for hundreds of years (through 'graph theory'), and more recently economists, sociologists and computer scientists have applied the mathematicians' insights to solve real-world problems.
There are many ways that understanding networks can help us become better digital marketers. A network algorithm, PageRank, underlies Google’s ordering of search results and allowed the company to power ahead of less network-savvy search engines such as Lycos, AltaVista and Yahoo! in the late 90s.
Networks are also central to the way that Facebook allows users to see and now find content, for example through Graph Search.
Network analysis also helps us understand patterns of social interaction between users on blogs, forums, and social media sites.
The Econsultancy network
In our example Econsultancy Twitter network we queried the Twitter API to find the users who mentioned, or shared a link from, Econsultancy over an 8-day period, and then worked out the relationships between them.

A detail of the network map of 3,930 users sharing Econsultancy.com content on Twitter
An increasing range of tools – including BlueNod, BottleNose, and various social media listening tools – allow us to gather Twitter network data. There’s also a range of free and paid software (NodeXL, yEd, Gephi, Mathematica) that allows us to analyse and visualise this data once we have it.
The ‘edges’ in our Econsultancy network are follower relationships between the users. Twitter networks made of other kinds of edges are possible. For example, we could decide to create an edge when one user mentions another, or retweets something they have tweeted.
But a network of follow relationships contains the richest and most complete data – because users follow so many more users than they interact directly with, and a ‘follow’ is a vote of confidence – or at least an expression of interest – in the user who is followed.
It shows that someone cares about their opinion and wants to hear it. It also gives us a clue about the direction in which information flows through this group of people, from the followed to the follower.
The Econsultancy 'community of interest'
Just by looking at the Econsultancy network we can see something fairly remarkable.
The vast majority of users (99.26% to be exact, or 3,901 of 3,930) are bound together in a single group – or network ‘component’, to use the technical term.
Every user in this group is connected, either directly or indirectly through others, to every other user. Why should this large group of people who seemingly share nothing apart from having mentioned Econsultancy on Twitter be bound together like this?
There are a few arcane mathematical reasons that make it more likely, but the fundamental reason is that the people in the network are a ‘community of interest’, defined by a shared enthusiasm for digital marketing in general, and Econsultancy.com in particular.
Real-life communities tend to be bound together by geography (a school, a workplace, a city), but online communities of interest are much more frictionless.
The connectedness of all these people talking about Econsultancy is pretty remarkable, when you think about it, and should give us a clue that something important is going on just below the surface.
In future posts I’ll be showing how we can look at the Econsultancy network to work out who is most influential, and to identify communities and cliques. I’ll also show how a Twitter network model can help us tailor content so that it really resonates, and is disseminated as deep into the network as possible.
Suscribirse a:
Comentarios (Atom)

