En la teoría de grafos, un coeficiente de agrupación es una medida del grado en el que los nodos en un gráfico que tienden a agruparse juntos. La evidencia sugiere que en la mayoría de redes del mundo real , y en particular las redes sociales, los nodos tienden a crear grupos muy unidos que se caracterizan por una densidad relativamente alta de enlaces; esta probabilidad tiende a ser mayor que la probabilidad media de un lazo establecido al azar entre dos nodos (Holland y Leinhardt de 1971, [1] Watts y Strogatz, 1998 [2]).
Existen dos versiones de esta medida: la global y la local. La versión global fue diseñado para dar una indicación general de la agrupación en la red, mientras que el local, da una indicación de la incrustación de los nodos individuales .
Coeficiente de agrupamiento global
El coeficiente de agrupación mundial se basa en tripletes de nodos. Un triplete consiste en tres nodos que están conectados por cualquiera de los otros dos (triplete abierto) o tres (triplete cerrado) lazos no dirigidos. Un triángulo se compone de tres tripletes cerrados, uno centrado en cada uno de los nodos. El coeficiente de agrupación global es el número de tripletes cerrados (o 3 x triángulos) sobre el número total de tríos (tanto abierto como cerrado). El primer intento de medir que fue hecha por Luce y Perry (1949). [3] Esta medida da una indicación de la agrupación en el conjunto de la red (global), y se puede aplicar tanto a las redes no dirigidas como dirigidas (a menudo llamadas transitividad, ver Wasserman y Faust, 1994, página 243 [4]).
Watts y Strogatz definen el coeficiente de agrupamiento como sigue, "Supongamos que un vértice
tiene 
vecinos; entonces un máximo de hasta 
enlaces pueden existir entre ellos (esto ocurre cuando cada vecino de está conectado a cada otro vecino de ). Sea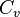 
la fracción de estos enlaces permitidos que existen actualmente. Definamos 
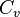como el promedio de sobre todos los ."Cociente de transitividad
El cociente de transitividad es un concepto relacionado. Se define como:
El coeficiente de agrupamiento asigna mayor peso a los nodos con menor grado, mientras que el cociente de transitividad asigna mayor peso a los nodos con mayor centralidad de grado.
Una generalización de redes ponderados fue propuesto por Opsahl y Panzarasa (2009), [5] y una redefinición de las redes de dos modos (tanto binaria y ponderadas) por Opsahl (2009). [6]
Coeficiente de agrupación local
.png)
Ejemplo: El coeficiente de la agrupación local de un grafo no dirigido. El coeficiente de agrupación local del nodo azul se calcula como la proporción de las conexiones entre sus vecinos que en realidad se realizan en comparación con el número de todas las conexiones posibles. En la figura, el nodo azul tiene tres vecinos, que pueden tener un máximo de 3 conexiones entre ellos. En la parte superior de la figura se observan las tres conexiones posibles (segmentos negros gruesos), dando un coeficiente de la agrupación local de 1. En la parte media de la figura se realiza sólo una conexión (línea de color negro de espesor) y 2 conexiones se echa en falta (líneas de puntos rojos), dando un coeficiente de clúster local de 1/3. Por último, ninguna de las posibles conexiones entre los vecinos del nodo azul se realizan, la producción de un valor de coeficiente de la agrupación local de 0.
El coeficiente de la agrupación local de un vértice (nodo) en un gráfico cuantifica qué tan cerca sus vecinos están de ser una camarilla (gráfico completo). Duncan J. Watts y Steven Strogatz introdujeron la medida en 1998 para determinar si un grafo es una red de mundo pequeño.
formalmente consiste de un conjunto de vértices 
y un conjunto de enlaces 
entre ellos. Un enlace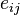 
conecta al vértice 
con el vértice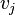 
.El vecindario
para un vértice es definido como sus vecinos inmediatamente conectados como sigue:
Definimos
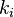como el número de vértices, 
, en el vecindario, , de un vértice.El coeficiente de agrupamiento local
para un vértice es entonces dado por la proporción de enlaces entre los vértices dentro de su vecindario dividido por el número de enlaces que podría potencialmente existir entre ellos. Para un grafo dirigido, 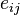es distinto de 
, y por lo tanto para cada vecindario hay 
enlaces que podrían existir entre los vértices dentro del vecindario (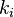 es el número de vecinos de un vértice). Entonces, el coeficiente de agrupamiento local para grafos dirigidos está dado por [2]
Dado que un grafo no dirigido tiene la propiedad que
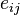y son idénticos. Por ello, si un vértice tiene 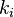vecinos, 
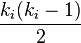enlaces podrían existir entre los vértices dentro de su vecindario. Por ello, el coeficiente de agrupación local para grafos no dirigidos puede ser definido como
Sea
el número de triángulos sobre 
para un grafo no dirigido 
. Esto es, es el número de subgrafos de con 3 enlaces y 3 vértices, uno de los cuales es . Sea 
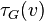el número de of tripletes sobre 
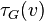. Esto es, es el número de subgrafos (no necesariamente inducidos) con 2 enlaces y 3 vértices, uno de los cuales es y tal que es incidente a ambos enlaces. Entonces podemos también definir al coeficiente de agrupamiento como 
Es simple demostrar que las dos definiciones precedentes son lo mismo, dado que
Estas medidas son iguales a 1 si cada vecino conectado a
se encuentra también conectado a cada otro vértice dentro del vecindario, y 0 si ningún vértice conectado a se conecta con ningún otro vértice que está conectado a .Coeficiente de agrupamiento medio de red
El coeficiente de agrupamiento para toda la red está dada por Watts y Strogatz [2] como la media de los coeficientes de la agrupación locales de todos los vértices
:[7]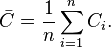
Un grafo es considerado un mundo pequeño, si el coeficiente de agrupamiento medio
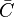es significativamente más alto que un grafo aleatorio construido con el mismo conjunto de vértices y si el grafo tiene aproximadamente la misma longitud media de camíno más corto que si correspondiente grafo aleatorio.Una generalización para grafos ponderados fue propuesta por Barrat et al. (2004),[8] y una redefinición para grafos bipartitos (también llamadas redes de dos modos) por Latapy et al. (2008)[9] y Opsahl (2009).[6]
Esta fórmula no es, por definición, definida para grafos con vértices aislados; ver Kaiser, (2008)[10] y Barmpoutis et al.[11] Las redes con los coeficientes de agrupamiento medio más grandes posible se encuentran que tienen estructuras modulares y al mismo tiempo, tiene la menor distancia media posible entre los diferentes nodos.[11]
Referencias
- P. W. Holland and S. Leinhardt (1971). "Transitivity in structural models of small groups".Comparative Group Studies 2: 107–124.
- D. J. Watts and Steven Strogatz (June 1998). "Collective dynamics of 'small-world' networks". Nature 393 (6684): 440–442. Bibcode:1998Natur.393..440W.doi:10.1038/30918. PMID 9623998.
- R. D. Luce and A. D. Perry (1949). "A method of matrix analysis of group structure". Psychometrika 14 (1): 95–116.doi:10.1007/BF02289146. PMID 18152948.
- Stanley Wasserman, Kathrine Faust, 1994. Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.
- Tore Opsahl and Pietro Panzarasa (2009). "Clustering in Weighted Networks". Social Networks 31 (2): 155–163.doi:10.1016/j.socnet.2009.02.002.
- Tore Opsahl (2009). "Clustering in Two-mode Networks". Conference and Workshop on Two-Mode Social Analysis (Sept 30-Oct 2, 2009).
- Kemper, Andreas (2009). Valuation of Network Effects in Software Markets: A Complex Networks Approach. Springer. p. 142.ISBN 9783790823660.
- A. Barrat and M. Barthelemy and R. Pastor-Satorras and A. Vespignani (2004). "The architecture of complex weighted networks".Proceedings of the National Academy of Sciences 101 (11): 3747–3752. arXiv:cond-mat/0311416. Bibcode:2004PNAS..101.3747B.doi:10.1073/pnas.0400087101. PMC 374315. PMID 15007165.
- M. Latapy and C. Magnien and N. Del Vecchio (2008). "Basic Notions for the Analysis of Large Two-mode Networks". Social Networks 30(1): 31–48. doi:10.1016/j.socnet.2007.04.006.
- Marcus kaiser (2008). "Mean clustering coefficients: the role of isolated nodes and leafs on clustering measures for small-world networks".New Journal of Physics 10 (8): 083042. arXiv:0802.2512. Bibcode:2008NJPh...10h3042K. doi:10.1088/1367-2630/10/8/083042.
- D. Barmpoutis and R. M. Murray (2010). "Networks with the Smallest Average Distance and the Largest Average Clustering".arXiv:1007.4031 [q-bio.MN].
