Scopus Maps
The base map of aggregated citation relations among 19,600 journals in Scopus during 2012 is as follows:
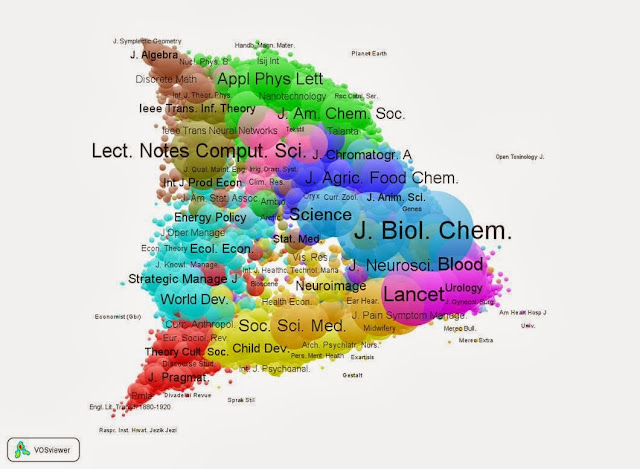
Figure 1: Base map of aggregated citation relations among 19,600 journals included in Scopus 2012; colors correspond to 27 communities distinguished by VOSviewer; This map can be web-started at
http://www.Vosviewer.com/Vosviewer.php?map=http://www.leydesdorff.net/scopus12/basemap.txt
One can generate an overlay for any set downloaded from Scopus as follows:
· Search in Scopus (advanced or basic); for example, using the search string ‘TITLE(“humanities computing”) OR TITLE(“computational humanities”) OR TITLE(“digital humanities”) OR TITLE(“ehumanities”) OR TITLE(“e-humanities”)’ provided 114 documents on October 8, 2013;
· Make a possible selection of records among the retrieved documents or tick “All”;
· Click on “Export”;
· Among the output formats, choose the “RIS format (Reference Manager, Procite, Endnote)” and “Specify fields to be exported”;
· Only “Source titles” should be exported; untick all other fields;
· Click on “Export”: the file “scopus.ris” can be saved; for example,
for the 114 records mentioned;
· Save the file “scopus.ris” in the same folder as the routine
overlay.exe and the file with the mapping information
scopus.dbf (right-click for saving this file). One can paste different (e.g., sequential) output files of Scopus into a single file, but the routine expects an input file with the name “scopus.ris”.
· One can now run overlay.exe in that same folder; preferably from the C-prompt; (using the C-prompt, one obtains error messages);
· The file “overlay.txt” (e.g.,
ehum.txt) is a map file that can be opened in
VOSviewer;
· Rao-Stirling diversity is stored in the file “rao.txt” and shown on the screen; overlay.dbf contains the information such as the number of publications in each journal.
The resulting overlay map reads as follows:
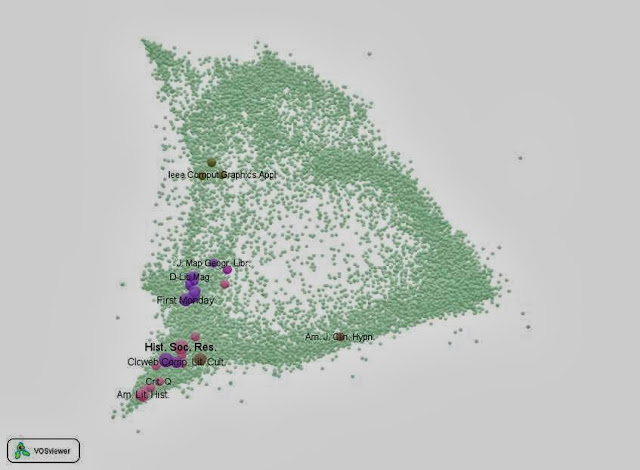
Figure 2: Overlay of 114 documents with the search string ‘TITLE(“humanities computing”) OR TITLE(“computational humanities”) OR TITLE(“digital humanities”) OR TITLE(“ehumanities”) OR TITLE(“e-humanities”)’ in Scopus; Rao-Stirling diversity = 0.1244. This map can be web-started at
http://www.Vosviewer.com/Vosviewer.php?map=http://www.leydesdorff.net/scopus12/ehum.txt&label_size=1.35
See for more explanation: Loet Leydesdorff, Félix de Moya-Anegón, and Vicente P. Guerrero-Bote, “Journal Maps, Interactive Overlays, and the Measurement of Interdisciplinarity on the basis of Scopus data” (in preparation).







 Google ordena los resultados de la búsqueda utilizando su propio algoritmo PageRank. A cada página web se le asigna un número en función del número de enlaces de otras páginas que la apuntan, el valor de esas páginas y otros criterios no públicos.
Google ordena los resultados de la búsqueda utilizando su propio algoritmo PageRank. A cada página web se le asigna un número en función del número de enlaces de otras páginas que la apuntan, el valor de esas páginas y otros criterios no públicos. es el PageRank de la página A.
es el PageRank de la página A.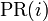 son los valores de PageRank que tienen cada una de las páginas i que enlazan a A.
son los valores de PageRank que tienen cada una de las páginas i que enlazan a A.
