Visualización de redes: Más allá de la bola de pelos

Visualizing Networks: Beyond the Hairball from OReillyStrata

Amargo Twitter de campañas políticas

Beyond "Bitter Twitter": Crowd-Photography for the Cyber-Tahrir Square

BY MICAH L. SIFRY | Tuesday, July 10 2012 - TechPresident

 A close-up view of @davidaxelrod's Twitter footprint from July 6, 2012

"This election may be remembered as the Bitter Twitter campaign," former Bush adviser Mark McKinnon said recently. With both campaigns avoiding offering any big new ideas, he predicted that "we are likely to see the next [few] months as a furious and relentless exchange of messages that aren't much longer or deeper than 140 characters."

Is that all that can be said about the daily Twitter wars between the Romney and Obama camps? To get a bigger picture — or rather, as you will see below, to get several bigger pictures — I turned to Marc A. Smith, chief social scientist with the Connected Action consulting group, who has long studied computer-mediated collective interaction. For the last few years, he and his colleagues have been doing what he chirpily calls "crowd photography for the cyber-Tahrir Square," using a sophisticated network mapping tool called NodeXL they've developed as a free extension to Excel. And the graphs they make offer a whole new way of seeing the connections among people, events and ideas as they coalesce online. Here, for example, is the conversation online when the "pink slime" controversy was at its height. Here's a chatter map for the controversy over "Fast and Furious"when Attorney General Eric Holder and Rep. Darrell Issa recently locked horns.

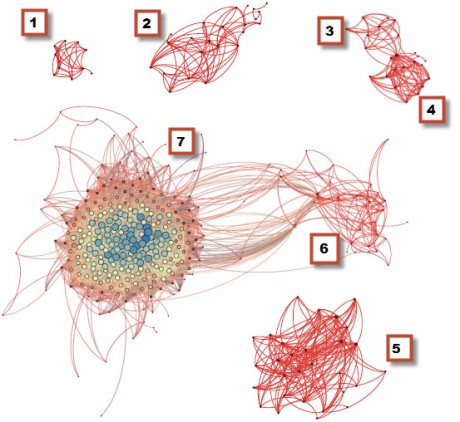
But how to read them? Take this snapshot of the public conversation on Twitter after the first day of this year's Personal Democracy Forum conference. Here, Smith got data on 711 Twitter users whose recent tweets contained the hashtag "#pdf12." Users are clustered together if they have lots of connection to each other, based on who follows whom, who replies to whom, and who mentions whom, and then each cluster is given its own rectangle based on those users having used similar hashtags in addition to #pdf12, with those listed in order of prominence.

Blue lines are links NodeXL builds when one user mentions, replies to or retweets another. Green lines represent people who follow each other. The "isolates" — in this case in the bottom right — are users who don't connect to others on the graph. "Reading" the graph (which I did with Smith's help), you can learn several things about the social landscape of the #PDF12 community.

There are three major subgroups that were tweeting from and about PDF12. First and largest, in the top left corner, are the open-government folks, whose top three hashtags after #PDF12 were #opengov, #opendata and #OGP (for the Open Government Partnership). At the center of this cluster, not surprising, you can see the Twitter avatars of power-tweeters like O'Reilly Media's Alex Howard (@digiphile), who covers open government and open data on a daily, even hourly, basis.

The second group in the top left are the PDF progressives, netroots folks who had likely just attended the annual Netroots Nation conference in Providence, RI. Their usage of hashtags like #NN12 and #ows (Occupy Wall Street) is a sure giveaway of their closeness to each other.

And third, in the bottom left corner of the graph, are the PDF netheads (you can recognize Zeynep Tufekci @techsoc, for example) who were paying closest attention to issues like online privacy, SOPA and PIPA.

A few additional observations are in order. First, there's not a lot of hierarchy to this community of individuals. There are lots of bilateral connections between people, as evinced by all the crosshatching green and blue lines. Second, the relatively large number of "isolates" in the bottom right corner is a good sign, Smith told me. It suggests that #PDF12 was also reaching beyond its core audience, and shows that we're not a completely "built-out" network. In other words, that there's room for growth. Network maps for other conferences, he says, often show that they're just speaking to themselves. And finally, the small cluster at the bottom of the middle of the graph indicates that there were probably some people using "pdf12" in their tweets during the conference who had absolutely nothing to do with the event, but maybe had some other common point of contact, such as linking to this document: http://www.eluniversal.com.mx/graficos/pdf12/recuento-eleccion.pdf.

Axelrod vs Fehrnstrom
Now take a look at how the Twitter conversation coalesces around two leading online surrogates for the Obama and Romney campaigns, David Axelrod and Eric Fehrnstrom. Axelrod is the Obama campaign's senior strategist; Fehrnstrom is one of Romney's senior campaign advisors. I asked Smith to run NodeXL against a recent list of Twitter users who either mentioned @davidaxelrod or @ericfehrn, and this is what he found.

Obviously, Axelrod's network is different than Fehrnstrom's. He has more than 103,000 followers on Twitter, compared to Fehrnstrom's 13,000. And he tweets more often, roughly 5-6 times a day, while Fehrnstrom tweets at most two or three times. As a result, their NodeXL graphs cover very different time periods. For Axelrod, it just took 13 hours on July 6th to accumulate 790 users who mentioned "davidaxelrod" in a tweet. It took 10 days, from June 27 thru July 6, to accumulate a similar number (876, actually) of users who mentioned "ericfehrn."

Here's the snapshot of Axelrod's Twittersphere around July 6th. You can view a high-definition "zoomable" version of the graph here.

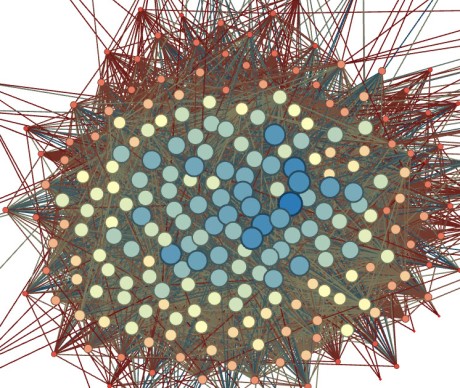
What's immediately apparent from the network of Axelrod mentioners is a) how polarized it is, and b) how much the pro-Obama side looks like a broadcast network, while the anti-Obama side looks like a dense community. The polarization isn't surprising; Smith says this pattern repeats across many NodeXL scans on topics touching on American politics. The most active people in online politics are from the passionate poles of our two-party system; this is not news, but there are some hints in these particular graphs that the online right is different than the online left, at least on Twitter. More on that in the moment.

First, the pro-Obama side, which is distinguished by people using Obama-friendly hashtags like "yeswewill" and "bettingonAmerica" as well as anti-Romney terms like "bainmitt" and "whatsmitthiding." If you zoom in closely on the people near Axelrod who are interrelated (the green clump in the upper right quadrant around him), you'll find other media players like Ben Smith (@buzzfeedben), Michael Scherer of Time (@michaelscherer) and Ben LaBolt, an Obama spokesman (@benlabolt). But the rest of the network of mentioners around Axelrod aren't part of the media insider circle--there are just lots of Twitter users who follow the Obama campaign's senior adviser who talk him up.

There's a lot of blue lines in this graph — remember, those are links NodeXL builds when one user mentions, replies to, or retweets another. Green lines represent people who follow each other. Given how well known Axelrod is on Twitter, it's not surprising to find so many people who mention him but don't follow each other — hence the prominence of the blue over the green. This is another indication that his reach online is more like a broadcast network or a brand than an interlaced community.

"There is an 'audience' cluster and two 'community' clusters," Smith explains. "Most blue lines (replies, mentions, retweets) point in to the 'community' clusters in which there is significant amounts of mutual connection. The community clusters are dense, while the broadcast or audience cluster is sparse with little interconnection. Axelrod has a powerful broadcast ability and his messages reverberate within the community clusters."

On the top right we have people who are good bets to be anti-Obama, given their prominent use of the "top conservatives on Twitter" hashtag #tcot, as well as anti-Obama terms like "fastandfurious" — a reference to the Justice Department scandal — and "obamatax." This group has no obvious hub, but it's also densely inter-connected. This is typical of conservatives who are heavy Twitter users; a lot of people joined the service starting in early 2007 who were looking for new leadership on the right, and along the way they all found each other.

Now let's look at Eric Fehrnstrom's Twittersphere. A zoomable version is here.

As noted above, comparing Fehrnstrom's online footprint to Axelrod's isn't apples-to-apples. He's not as well-known, he's not on TV as often, and he isn't as big a Twitter user. Unfortunately for the purposes of this article, there isn't an exact parallel to Axelrod in the Romneyverse, at least when it comes to their online activities. So, caveat emptor, this isn't meant to suggest that what one man is doing online is somehow "better" than the other. They're each interesting but for somewhat different reasons.

Again, the most obvious finding from looking at people mentioning "ericfehrn" on Twitter is that they're a polarized group. The ones on the left hand side of the graphic are mostly pro-Romney; the ones on the right are mostly pro-Obama. We know this from the hashtags they're using in common: "obamacare," "obamatax" "fullrepeal" and "teaparty" for the Romneyites; and "p2" "aca" and "whatisromneyhiding" for the Obamanauts. (Smith has noticed that few Republicans ever say "Affordable Care Act," by the way.) On the Obama side of the split, you can zoom in and find individuals like Donna Brazile and Paul Begala, well-known Democratic partisans; on the other side you can find GOP stalwarts like Matt Lewis and Justin Hart.

Interestingly, you can see some signs of Fehrnstrom having a small "broadcast" footprint in the arc-like groups of Twitter users on the outer edge of the left-hand cluster. These are people like the much bigger circle around Axelrod, who mention or retweet things that "@ericfehrn" says, but who aren't really connected in a more intensive way as a community of people who know each other.

Don't Think of an Echo Chamber
When I first reached out to Smith, I thought that mapping the Twitter relationships of political power players like Axelrod and Fehrnstrom might demonstrate just how much Twitter was intensifying the insider culture of Washington and elite politics, to the chagrin of people like Mark McKinnon. But after looking at these graphs, I'm not so sure that that is the only thing going on with Twitter and the presidential campaigns.

Yes, there are a lot of A-list types showing up on these two graphs, the sort of people who have given the Washington-centric White House Correspondents Dinner its current reputation as the "nerdprom" for the media-politics elite, plus some hardworking journalists who are just doing their jobs. But at the same time, there's a much bigger network of influential voices in the political Twittersphere around the Romney and Obama camps, as is reflected by centrality in the graphs of people like @ttjemery ("Christian and conservative" with 29,000 followers), @daggy1 (a self-described "enemy of socialism" with 27,000 followers), or @gaypatriot ("America's leading gay conservative voice"). And this active and highly networked set of people clearly leans right; none of the top independent progressives on Twitter happen to show up as significant participants in these two snapshots.

What that suggests is that after you get past the daily "Bitter Twitter" back-and-forth games that these campaigns surrogates are playing with each other and the Beltway media, there's a large secondary group of political activists, most of them conservatives, who are also engaged in chewing on the daily give-and-take of the presidential campaign. A lot of these people know and relate to each other via Twitter. If progressive activists were as engaged on Twitter, then presumably we'd see the same kind of dense green cloud in interconnections around Axelrod on the pro-Obama side of his graph as we do for Fehrnstrom on the pro-Romney side of his. Arguably, the fact that Axelrod is much more of a "celebrity" online may explain some of this difference too.

NodeXL is a powerful tool for exploring the social landscapes of public conversations about all kinds of topics, but it takes time and effort to develop the visual literacy needed to make sense of these graphs. Or, as Smith puts it, "it takes time to go from seeing something that looks like bug splatter on my windshield to 'oh, that looks interesting.'" Over the coming months, we're going to keep exploring this terrain with Smith's help, as he has kindly offered to run some queries on techPresident's behalf. (He also does customized research for a modest fee.) What would you like to explore? We can visualize the network around a person or group of people, a term or hashtag, even a url. The zeitgeist awaits.

Visualizando Facebook

Super Fan Facebook Graph

It’s pretty common to have a Facebook graph that consists of a few unconnected or only loosely connected clusters. In the visualization above there are distinct “constellations” of people I play cards with, people I worked with at Microsoft, people I am related to, people I went to high school with, and people I went to college with. Most of the people in those groups are fairly interconnected with each other but not at all connected to people in the other groups, or perhaps only loosely connected. For example the two nodes between 3 and 4 are my brothers who went to the same high school as me and therefore bring the high school and family clusters into proximity, but they aren’t connected to anyone I went to college with or have worked with in the past 10 years. Those clusters are the type of graphs I’d expect to see from the organic use patterns of a typical Facebook users, more or less.

So what’s with the really big blob? That’s the social network of someone who behaves like a very, very passionate fan of reality TV, in particular Big Brother and Survivor. I’ve been managing social media around theBig Brother Live Feeds for a while, and like my customers, I’ve connected to lots of stars and tons of fans. And all of those folks are connected to each other through multiple connections themselves. Over in constellation 6 are people I’ve worked with at RealNetworks, and the nodes connecting that group to super fan cluster are folks who work directly with customers, like our chat room moderators, my social media team, editors and video hosts, as well as some key folks in program management and operations.

Here’s the key if you’re curious

1. Bridge players
2. Microsoft friends (past gig)
3. High school friends
4. Family
5. Knox College friends
6. RealNetworks (current gig)
7. Reality TV fans

Aside from the density of connections, you can see by the size of the circle which nodes are highly connected. The average number of connections in the graph is 55 but that average is thrown off by the folks represented by the very large circles, who have between 150 and 200 connections each. Some of those are stars who have been on the shows–and reality stars tend to be very accessible and connected on both Facebook and Twitter. They don’t just accept friend requests from fans, they will actively and frequently engage. However, it’s worth pointing out that some of the most connected members of my graph are just fans. They are the type of fans who will travel to Las Vegas after the season is over to party with the stars. They know each other very well and are as connected and influential in the fan community (and among my customer base) as any of the stars or casting directors.

Here’s a close up of the Reality TV fans

And here are the high school / family clusters so you can see just how much sparser the connections are

Note: This post was an extension of the first week’s lesson of the Coursera course Social Network Analysis taught by Lada Adamic. Thanks, Lada!  The visualization tool I used is Gephi.

Performing Statements

Redes de amor adolescente

Love is a Battlefield Spanning-Tree Network with no 4-Cycles

by KIERAN HEALY

Quick, in high school were you ever told not to date your old girlfriend’s current boyfriend’s old girlfriend? Or your old boyfriend’s current girlfriend’s old boyfriend? Probably not. But I bet you never did, either. This month’s American Journal of Sociology has a very nice paper (subscription only, alas) by Peter Bearman, Jim Moody and Katherine Stovel about the structure of the romantic and sexual network in a population of over 800 adolescents at “Jefferson High” in a midsized town in the midwestern United States. They got a pretty well-bounded population (a high school included in the AddHealth study) and mapped out all the connections between the students. Read on for the lurid details.

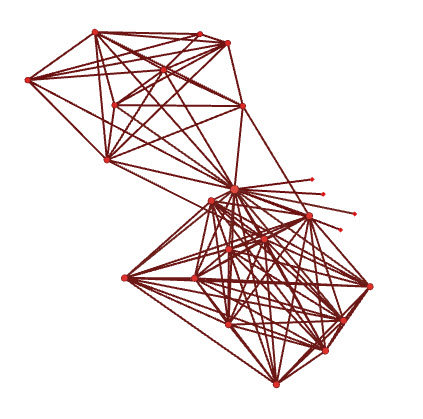
The authors found that the observed network isn’t well-represented by existing models, which are mainly concerned with predicting how STDs propagate through populations and have often been based on ego-centered network data. These are surveys where you ask the respondents about their sexual networks, but the respondents aren’t necessarily in the same network. Here’s a picture of four kinds of network:

Core models posit a small group of very sexually-active individuals who occasionally come into contact with (and infect) those outside the core. Bridge models think in terms of an infected component and an uninfected component which join at some point. The biggest network component observed at Jefferson High turned out to be the fourth type, however: a “spanning tree” structure. This is “a long chain of interconnections that stretches across a population, like rural phone wires running from a long trunk line to individual houses … characterized by a graph with few cycles, low redundancy, and consequently very sparse overall density.” When they tried to simulate this bit of the graph structure, the authors found they could get most of the way there using a simple model where the probability of a tie depended on individuals having a preference for others with the same amount of sexual experience as themselves.[1] But simulated networks based on this model didn’t quite match the properties of the observed network. In particular, while the simulations had cycles of length 4, the Jefferson High network did not.

What’s a cycle? If you start at Crooked Timber and click over to Dan Drezner and then click Dan’s link to Mark Kleiman and then return to Crooked Timber via Mark’s link to us, you’ve completed a cycle of length 3: a walk through the network that starts and ends with the same actor and where all the other actors are different and not repeated along the way. Cycles of length 3 are the smallest possible cycles. When it comes to tracing paths through heterosexual relationships, though, the smallest possible cycles are of length 4. In order to make a cycle beginning and ending with yourself, you need two members of the opposite sex plus one intervening individual the same sex as you. It turns out that this kind of cycle is just not found in the Jefferson High network. Although there’s no explicit taboo or social norm against that kind of pattern, nevertheless people just don’t date their old partner’s current partner’s old partner.

From the perspective of males or females (and independent of the pattern of “rejection”), a relationship that completes a cycle of length 4 can be thought of as a “seconds partnership,” and therefore involves a public loss of status. Most adolescents would probably stare blankly at the researcher who asked boys: Is there a prohibition in your school against being in a relationship with your old girlfriend’s current boyfriend’s old girlfriend? It is a mouthful, but it makes intuitive sense. … For adolescents, the consequence of this prohibition is of little interest: what concerns them is avoiding status loss. But from the perspective of those interested in understanding the determinants of disease diffusion, the significance of a norm against relationships that complete short cycles is profound. The structural impact of the norm is that it induces a spanning tree, as versus a structure characterized by many densely connected pockets of activity (i.e., a core structure).

Individuals constitute social structures, yet those structures have properties that the members do not know about and can’t easily grasp—our vast amount of folk knowledge about our social relations notwithstanding. These properties can have all kinds of serious consequences. The “No 4-cycles” rule is interesting because on the one hand it reflects a very simple bit of structure and it’s not something that’s prohibited in any strong normative sense. I’m not sure I buy the authors’ status-based explanation for it, though. They suggest some alternatives—“’jealousy’ or the avoidance of too much ‘closeness,’ a sentiment perhaps best described unscientifically as the ‘yuck factor.’” I find the yuck-factor idea more intriquing: I wonder whether it’s more likely to show up at the limits of easily-described network structures. Bigger cycles defy easy verbal description altogether and are also subject to lack of information because some of the ties will be in the past or far away, so they’re not subject to avoidance. Dyadic ties are easy to keep track of. Short cycles are still tricky to grasp, but it’s not that hard, so being able to trace them triggers the taboo-like “yuck” response.

As for consequences, the spanning-tree structures created by experience homophily plus the 4-cycle rule are very effective at propagating diseases along their chains. But they are also easy to break in a way that core-type networks are not:

Under core and inverse core structures, it matters enormously which actors are reached, while under a spanning tree structure the key is not so much which actors are reached, just that some are. This is because given the dynamic tendency for unconnected dyads and triads to attach to the main component, the structure is equally sensitive to a break (failure to transmit disease) at any site in the graph. In this way, relatively low levels of behavior changeeven by low-risk actors, who are perhaps the easiest to influence can easily break a spanning tree network into small disconnected components, thereby fragmenting the epidemic and radically limiting its scope.

fn1. Homophily, or the tendency do associate with others with similar traits to oneself, is a powerful social force that explains a great deal about the structure of social networks—in this case, homophily on experience.

Crooked Timber

Influencia en comunidades

Community Influencers Step by Step

by MikeW 

Michael Wu, Ph.D. is Lithium's Principal Scientist of Analytics, digging into the complex dynamics of social interaction and online communities.

He's a regular blogger on the Lithosphere and previously wrote in the Analytic Science blog.

You can follow him on Twitter at mich8elwu.

---

Suppose you need to find the influencers for your brand in a community, how would you go about doing this? What kind of data do you need, and where do you start? Good question, today I am going to show you, step by step, how to find influencers in anonline community. I will use Lithium’s own online community, Lithosphere, in the following example, but you can do the same with any social media platform.

1. Identify the Necessary Data

From my earlier post “Finding the Influencers,” we know that an influencer must have high bandwidth and be credible. For finding high bandwidth users, our platform tracks participation velocity data for each user, and also collects a variety of social equity data. Our community platform also allows users to specify friends in the community. However, this feature is more common in enthusiasts’ communities than in other types of sites, so we have only a small amount of data to construct the friendship graph.

For finding credible users, we have reciprocity data (e.g. kudos and accepted solutions) and reputation data from our reputation engine. However, because our community platform does not require users to build an extensive user profile, we do not have self-proclaimed data on interest and expertise. As mentioned above, we probably do not have enough data to construct a reliable friendship graph, but friendship graph is less useful for finding credible users anyway. Since our community is a highly interactive platform with many topic-specific conversations among users, we can build a topic-specific conversation graph from the conversation data. Social network analysis (SNA) can then be applied to this social graph to accurately identify influencers.

From our analysis, we can see that our community platform has plenty of data for finding influencers, and we can pick and choose what data we would like to use. This may not be true on other platforms or other social media channels. As Philalluded to in his post, I took the SNA approach because it allows us to identify influencers reliably -- furthermore, it allows us to identify different types of influencers (see Are all Influencers Created Equal?).

2. Build the Relevant Social Graph

Most of the conversations in a branded community will already be focused around the brand, so they are likely all relevant. This eliminates the need to filter out irrelevant content. However, to ensure temporal relevance (i.e. timing), we still need to filter out temporally irrelevant (i.e. old) content before we build the conversation social graph. To do this, I filtered out all conversations that are older than one month and use only the data within this one month window.

Within this relevant time window, I built the social graph by connecting two users if they have participated in a common conversation. So the relationship that is represented by the edges is co-participation in a conversation (recall that this edge relationship is the most important thing to keep in mind when reading social graphs). The conversation can be a thread in a forum, a blog article or an idea via comments. I also did something more sophisticated by computing the strength of connection between the two users, which is determined by three factors.

1. The connection strength in a conversation is proportional to the number of messages a user contributed to a conversation. The more messages they contribute, the more likely they will be seen and remembered.
2. The connection strength in a conversation is inversely proportional to the number of unique participants in the conversation. If there are more participants, then each user is less likely to be remembered.
3. The connection strength is then summed across all the conversations where the two users have co-participated. The more conversations a pair of users co-participated in, the stronger the connection between them.

The result is the conversation graph shown here. The data is from Lithosphere for the one month period between 2010-03-05 and 2010-04-05. I labeled the users with their screen name. I can see myself, MikeW, and see that I’ve co-participated in conversations with seven other Lithosphere members (Mark_Hopkins, jennyb, MikeTD, reinvent_ed, Laura, PhilS, and PaulGi).

Since I have the connection strength between users, I could also filter out weak connections if necessary (when there are too many conversations in a community and the social graph becomes too cluttered to read). In this case, I didn’t need to do this because Lithosphere is still a small community; there were only 57 registered users co-participating in conversations within the one month period of interest. However, keep in mind that this does not mean that only 57 users posted. A user can post, but if no one replies, then there is no co-participation.

3. Social Network Analysis of the Conversation Graph

Once the social graph is built, the ‘hard work’ is done. The rest is number crunching using SNA and interpreting the results. SNA analyzes the social graph and computes node metrics that rank the importance of each user in the network. However, there are many ways that a user can be important. Some are well connected (have many connections), some are reputable (recognized by other important people), yet others may still be important in subtle ways. So SNA actually computes a series of node metrics depending on how we want to measure importance.

Currently, I’ve implemented 10 different such node metrics:

1. Degree Centrality: How connected a user is, (depending on the edge relationship, this centrality measures the number of connections of a user -- friends, colleagues, etc.)
2. Eigenvector Centrality: How reputable and recognized is a user
3. PageRank Score: How much of an authority the user is (this is the same algorithm that Google uses to find authority web pages on the Internet)
4. Potential reach: How many people can the user reach within two degrees
5. Clustering Coefficient: How cliquish is the user (the probability that two of your friends are also friends with each other)
6. Betweenness Centrality: How critical is the user for information diffusion
7. Core Number: How central is the user in the network
8. Vertex Eccentricity: How far away from the center is the user
9. Closeness Centrality for the connected components: How close the user is to the rest of the connected component of the network
10. Closeness Centrality for all components: How close the user is to the entire network, including disconnected components

You do not have to know all of them, but you should try to understand the common ones, such as degree centrality, Eigenvector centrality, PageRank score, and potential reach. I can overlay these node metrics on the social graph by mapping them to the size and color of the vertices, so we can visually see these metrics along with the social graph.

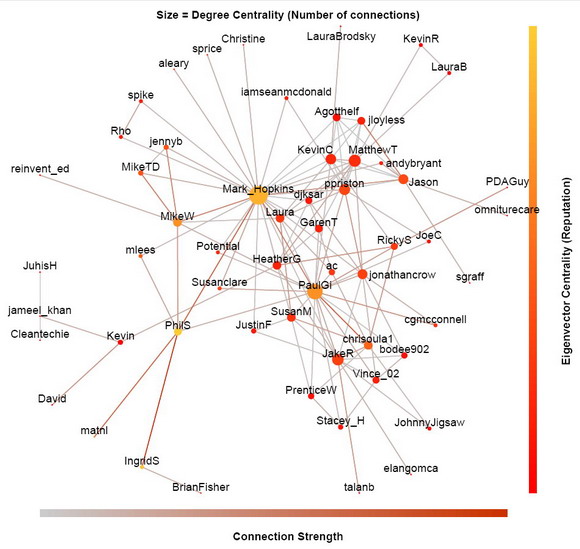
In the above social graph, I map the degree centrality (connectedness) to the size of the dots, and the eigenvector centrality (reputation) to their color. Clearly, Mark_Hopkins has the most connections as indicated by the biggest dot. However, PhilS is the most reputable as indicated by the most yellow color, even though he only talked to six users in that period. Although Mark_Hopkins, PaulGi, IngridS and I are not too far behind on the eigenvector centrality scale, the reason that PhilS is more reputable is because he has strong connections with other users (indicated by the brown edges) and that he is connected to a lot of other reputable users. Remember, how connected a user is does not necessarily correlate with his reputation.

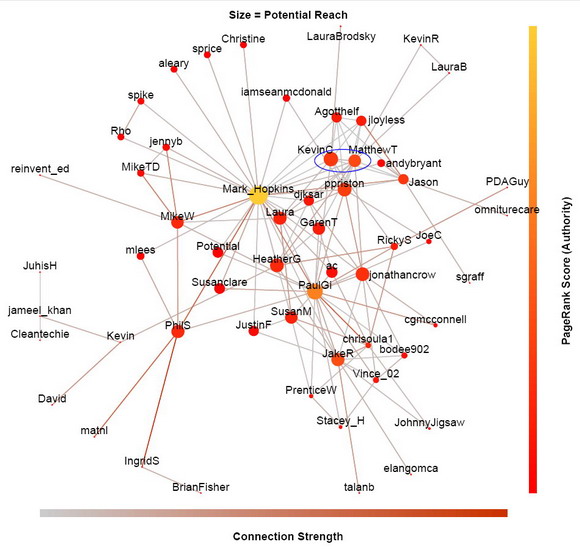
In this version of the social graph (above), I map the potential reach metric to the size of the dots, and the PageRank score to their color. Again, Mark_Hopkins has the greatest reach and the highest PageRankScore for the past month. But reach and authority is not always correlated either. For example, KevinC has greater reach than MatthewT in Lithosphere (KevinC is bigger dot), but MatthewT has higher authority than KevinC (MatthewT’s dot has more yellow tone).

I must emphasize that these ranking are only relevant for about a month window, because I have restricted the computation from 2010-03-05 to 2010-04-05. If we plot the social graph today, these node metrics could well be very different. So if you start participating more today, you may be one of the biggest and most yellow dots a month later.

Since Lithosphere is a pretty small community, most of these node metrics are quite well correlated. This will not be the case for larger communities. Therefore, depending on your marketing needs and constraints, you will need help from different kind of influencers in the community (see Are all Influencers Created Equal?).

Next week is our Lithium Network Confernece (LiNC2010). I will be there, so please come by and say hello if you will be attending. If not, we can always meet here at Lithosphere. Unless there are some special request at LiNC, I plan to show you some more social graphs from larger communities. But for now, I welcome any questions and comments as usual. See you next week at LiNC2010 or here at Lithosphere.

Lithosphere

Estadísticos y agrupamiento de grafo

Graph statistics and graph clustering

Participants : Daniel Archambault, Romain Bourqui, Maylis Delest, Frédéric Gilbert, Guy Melançon, François Queyroi, Arnaud Sallaberry, Paolo Simonetto, Faraz Zaidi.

Community detection in static networks

Searching of information on the web is a frequent task requiring some sort of organization to facilitate the searching process. Often this information is distributed, semistructured, overlapping and heterogeneous. Organization and structuring this information is an active area of research where the goal is to help users locate required information efficiently. Clustering is a well known technique to group similar information. Although often described as the unsupervised learning, clustering is quite trivial, as it often requires human intervention in terms of a number of parameters to guide the process. We address the clustering problem of web pages where the goal is to organize information to facilitate users for faster access to required information. In [30] We introduce a hierarchical fuzzy clustering algorithm to organize web pages. The algorithm uses a topological decomposition on the co-occurrence network of keywords to devise heuristics which help determine the input parameters for our clustering algorithm. Finally, we compare the results of the proposed algorithm with existing algorithms in the literature.

The exponential growth of data in various fields such as Social Networks and Internet has stimulated lots of activity in the field of network analysis and data mining. Identifying Communities remains a fundamental technique to explore and organize these networks. Few metrics are widely used to discover the presence of communities in a network. We argue that these metrics do not truly reflect the presence of communities by presenting counter examples. This is because these metrics concentrate on local cohesiveness among nodes where the goal is to judge whether two nodes belong to the same community or vise versa. Thus loosing the overall perspective of the presence of communities in the entire network. In [29] , we propose a new metric to identify the presence of communities in real world networks. This metric is based on the topological decomposition of networks taking into account two important ingredients of real world networks, the degree distribution and the density of nodes. We show the effectiveness of the proposed metric by testing it on various real world data sets.

Community detection in dynamic social networks

Figure 7. Community detection in social networks – Framework overview

Detection of community structures in social networks has attracted lots of attention in the domain of sociology and behavioral sciences. Social networks also exhibit dynamic nature as these networks change continuously with the passage of time. Social networks might also present a hierarchical structure led by individuals who play important roles in a society such as managers and decision makers. Detection and visualization of these networks that are changing over time is a challenging problem where communities change as a function of events taking place in the society and the role people play in it. In [15] , we address these issues by presenting a system to analyze dynamic social networks (see Fig. 7 ). The proposed system is based on dynamic graph discretization and graph clustering. The system allows detection of major structural changes taking place in social communities over time and reveals hierarchies by identifying influential people in social networks. We use two different data sets for the empirical evaluation and observe that our system helps to discover interesting facts about the social and hierarchical structures present in these social networks.

In [35] we give the complete description of the graph decomposition algorithm used in [15] to generate overlapping clusters. The complexity of this algorithm is  . This algorithm is particularly efficient due to its ability to detect major modifications along dynamic processes such as time related ones.

Figure 8. Result of our decomposition algorithm on a subgraph of the "Hollywood graph" (actors graph) containing 421 movies. Our algorithm detected 404 of these movies.

Evaluation of clustering quality

Many real world systems can be modeled as networks or graphs. Clustering algorithms that help us to organize and understand these networks are usually referred to as, graph based clustering algorithms. Many algorithms exist in the literature for clustering network data. Evaluating the quality of these clustering algorithms is an important task addressed by different researchers. An important ingredient of evaluating these clustering techniques is the node-edge density of a cluster. We argue that evaluation methods based on density are heavily biased to networks having dense components, such as social networks, but are not well suited for data sets with other network topologies where the nodes are not densely connected. Example of such data sets are the transportation and Internet networks. We justify our hypothesis by presenting examples from real world data sets.

In [28] , we present a new metric to evaluate the quality of a clustering algorithm to overcome the limitations of existing cluster evaluation techniques. This new metric is based on the path length of the elements of a cluster and avoids judging the quality based on cluster density. We show the effectiveness of the proposed metric by comparing its results with other existing evaluation methods on artificially generated and real world data sets.

Figure 9. Air Traffic Network Drawn using Hong Kong at the center and some airports directly connected to it.

In [33] , We design and study a multilevel modularity quality for clustered graphs, explicitly taking the nesting structure of clusters into account. Multilevel models appear crucial in the natural and social sciences. The multilevel modularity quality measure generalizes a modularity quality measure introduced by Mancoridis in the context of reverse software engineering. The measure we designed recursively traverses the hierarchy of clusters and computes a one variable polynomial encoding the intra and inter-cluster connectivity ratios appearing at all levels in a hierarchical clustering. The resulting polynomial reflects how the graph combines with the hierarchy of clusters and can be used to assess the quality of a hierarchical clustering. We discuss examples as proof-of-concept.

INRIA

Efecto de red a través de componentes gigantes

"Giant Components" Implies WInner-Takes-All in the Social Network Race

In graph theoretic social networking analysis, there's a concept known as "Giant Components". As the name implies, in any given human social network, there exists one main, extremely large, set of connected "nodes" (people) surrounded by significantly smaller, disconnected from the giant component, peripheral clusters of social networks.

This is illustrated qualitatively in "Networks, Crowds, and Markets" (free version here) by given the example: consider your current friend group, and who they're connected to, and so on. Ultimately, you'll find you're indirected connected to people from other countries. Another way to put it, if everyone has 100 (unique) friends, you very quickly get to large numbers of connected nodes (100 of your friends x (have) 100 friends x (who have) 100 friends x (who have) 100 friends x (who have) 100 friends = 10B people. However, there will be people, isolated on an island somewhere, that is not connected to the giant component.

Random Example (from here). You can see that a high proportion of nodes below to one connected cluster.

If any one person, in any one of the smaller clusters, becomes connected to the "Giant Component", the entire cluster is then considered part of the "Giant Component". So, it's reasonable to assume that, at some point, the desert island person will eventually meet one person in the giant component. It seems, in this connected world, we're almost fatalistically destined to be part of the giant component.

It is inevitable then, that we become part of the Facebook giant component, right? They're nearing 600 millions users, and check out this giant component.

In reality, things aren't as inevitable. It's not obvious initially, but a few things to consider:

• The definition of the edges (connections between people) are a little more nuanced than simply "knowing" someone. What if you, instead of drawing a social graph based on Facebook-stated friendships, you drew it based on spending greater than 10 hours a day together? The graph would become much more fragmented.
• Graphs can be used to represent different classes of social graphs. For example, and Facebook even does this, my family, and my coworkers could be represented as separate graphs. In other words, people are capable of belonging to multiple networks.

Both of these facts create an opportunity for emerging or niche social networks to evolve and grow -- and not necessarily at the expense of Facebook either! In retrospect, Livemocha, an interest-based social network, benefited from this.

Another example (or maybe a 3rd bullet is required above stating "cultural norms") is Mixi, a Japanese social network. Recently featured in the NYTimes, Facebook has been relatively unsuccessful in Japan. Some speculate it is cultural in nature; that the Japanese are more private and that Facebook's religious-like fervor towards unfettered openness doesn't resonate there. Allegedly, on Mixi only 5% of users use their real picture as an avatar.

The "giant component" question seems to simply be one of definition. Existentially, or environmentally, aren't we all connected?

As an aside, I'm taking a Social Media Analysis reading course this semester (similar to this one at Carnegie Melon). I have a weekly blog-writing assignment - this is the first post of many. 

Social Graph Paper