ARS 101: Modularidad

Modularidad en redes

La modularidad es una medida de la estructura de las redes o grafos. Fue diseñado para medir la fuerza de la división de una red en módulos (también llamados grupos, agrupamientos o comunidades). Las redes con alta modularidad tienen conexiones sólidas entre los nodos dentro de los módulos, pero escasas conexiones entre nodos en diferentes módulos. La modularidad se utiliza a menudo en los métodos de optimización para la detección de la estructura comunitaria de las redes. Sin embargo, se ha demostrado que la modularidad sufre un límite de resolución y, por lo tanto, no es capaz de detectar pequeñas comunidades. Las redes biológicas, incluidos los cerebros animales, presentan un alto grado de modularidad.

Motivación

Muchos problemas científicamente importantes se pueden representar y ser empíricamente estudiados a través de redes. Por ejemplo, los patrones biológicos y sociales, la World Wide Web, las redes metabólicas, redes tróficas, redes neuronales y redes patológicos son algunos ejemplos de los problemas del mundo real que pueden ser representados matemáticamente y topológicamente estudiaron para revelar algunas características estructurales inesperadas. [1] La mayoría de estas redes poseen una cierta estructura de comunidad que tiene considerable importancia en la construcción de un entendimiento respecto a la dinámica de la red. Por ejemplo, una comunidad social estrechamente relacionado implicará una mayor velocidad de transmisión de información o rumor entre ellos de una comunidad mal conectados. Por lo tanto, si una red está representado por un número de nodos individuales conectadas por enlaces que significan un cierto grado de interacción entre los nodos, las comunidades se definen como grupos de nodos densamente interconectados que son sólo escasamente conectados con el resto de la red. Por lo tanto, puede ser imprescindible identificar comunidades en las redes ya que las comunidades pueden tener propiedades muy diferentes, tales como grado, coeficiente de agrupamiento, intermediación, centralidad nodal [2], etc, respecto a la media de la red. La modularidad es una de tales medidas, que, cuando se maximiza, sino que conduce a la aparición de comunidades en una red dada.

Definición

La modularidad es la fracción de los enlaces que caen dentro de grupos dados menos el valor esperado que dicha fracción hubiese recibido si los enlaces se hubiesen distribuido al azar. El valor de la modularidad se encuentra en el intervalo [-.5,1). Es positivo si el número de enlaces dentro de los grupos supera el número esperado sobre la base de pura casualidad. Para una determinada división de vértices de la red en algunos módulos, la modularidad refleja la concentración de los nodos dentro de los módulos en comparación con distribución al azar de los enlaces entre todos los nodos, independientemente de los módulos.
Existen diferentes métodos para el cálculo de la modularidad. [1] En la versión más común del concepto, la aleatorización de los enlaces se realiza con el fin de preservar el grado de cada vértice. Veamos un grafo con  nodos y  enlaces (enlaces) de tal manera que el grafo se puede dividir en 2 comunidades usando una variable de membrecía   Si un nodo   pertenece a la comunidad 1, 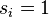  o si  pertenece a la comunidad 2,   Sea que la matriz de adyacencia de la red estará representado por A, donde 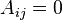 significa que no hay ninguna ventaja (sin interacción) entre los nodos i y j y  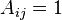significa que hay un enlace entre los dos. También por simplicidad consideramos una red no dirigida. Así   (Es importante tener en cuenta que pueden existir múltiples enlaces entre los nodos 2 y aquí evaluamos el caso más simple).
La modularidad Q se define entonces como la fracción de enlaces que caen dentro del grupo 1 o 2, menos el número esperado de enlaces dentro del grupo 1 y 2 para un grafo aleatorio con el mismo grado de distribución como el nodo de red determinado.
El número esperado de enlaces se calcula utilizando el concepto de modelos de configuración. [3] El modelo de configuración es una realización aleatoria de una red en particular. Dada una red con n nodos, donde cada nodo i tiene un grado nodal ${\displaystyle k_{v}}$, el modelo de configuración corta cada enlace en 2 mitades, y luego cada media punta, llamados a trozo, es reconectado al azar con cualquier otro ramal en la red, incluso permitiendo auto bucles. Por lo tanto, a pesar de que la distribución de grado de nodo del grafo permanece intacta, los resultados del modelo de configuración en una red completamente al azar.

Número esperado de enlaces entre nodos

Si el número total de ramales es ln


Ahora, si se selecciona al azar dos nodos i y j con grados nodo ki y kj respectivamente, y recablear los ramales a estos 2 nodos y, a continuación,

Número esperado de enlaces [enlaces completos entre i y j] = (enlaces completos entre i y j) / (número total de posibles reconexiones) (2)

Número total de reconexiones posibles = número de ramales que quedan después de la elección de un determinado ramal = ln- 1 = ln para n grande

Por lo tanto, se esperaba [Número de enlaces completos entre i y j] = (ki * kJ) / ln = (ki kJ) / 2m.
Por lo tanto, el número real de enlaces entre i y j menos el número esperado de enlaces entre ellos es Aij - (ki kj) / 2 m. Por lo tanto el uso de [1]



Es importante tener en cuenta que (3) es válido para la partición en sólo 2 comunidades. La partición jerárquica (es decir, partición en 2 comunidades, a continuación, las 2 sub- comunidades con particiones más en 2 comunidades más pequeñas sub sólo para maximizar Q) es un posible enfoque para identificar múltiples comunidades en una red. Además, (3) puede ser generalizada para la partición de una red en comunidades c. [4]


eii donde es la fracción de los enlaces con ambas vértices finales de la misma comunidad i:


y ai es la fracción de enlaces con al menos un extremo de vértice en la comunidad i :

Ejemplo de detección múltiple comunidad

Consideramos una red no dirigida con 10 nodos y 12 enlaces y la siguiente matriz de adyacencia.

Fig. 1. Red de muestra correspondiente a la matriz de adyacencia con 10 nodos, 12 enlaces.

Fig. 2. Particiones de red que maximizan Q. máxima Q = 0.4895

Nodo ID	1	2	3	4	5	6	7	8	9	10
1	0	1	1	0	0	0	0	0	0	1
2	1	0	1	0	0	0	0	0	0	0
3	1	1	0	0	0	0	0	0	0	0
4	0	0	0	0	1	1	0	0	0	1
5	0	0	0	1	0	1	0	0	0	0
6	0	0	0	1	1	0	0	0	0	0
7	0	0	0	0	0	0	0	1	1	1
8	0	0	0	0	0	0	1	0	1	0
9	0	0	0	0	0	0	1	1	0	0
10	1	0	0	1	0	0	1	0	0	0

Las comunidades en la gráfica están representados por los grupos de nodos de color rojo, verde y azul en la figura 1. Las particiones de la comunidad óptimos se representan en la figura 2.

Formulación matricial

Una formulación alternativa de la modularidad, útil en particular en algoritmos de optimización espectrales, es como sigue. [1] Definir Sir sea 1 si vértice i pertenece al grupo de r y cero en caso contrario. entonces


y por lo tanto


donde S es teniendo la matriz (no cuadrados) elementos Sir y B es la llamada matriz de modularidad, que tiene elementos



Todas las filas y columnas de la matriz de modularidad suma a cero, lo que significa que la modularidad de una red indivisa también es siempre cero.
Para redes divididas en sólo dos comunidades, se puede definir como alternativa si = ± 1 para indicar que la comunidad a la que pertenece el nodo i, que a su vez conduce a

,
donde s es el vector columna con elementos de SI. [1]
Esta función tiene la misma forma que el hamiltoniano de un vidrio de espín Ising, una conexión que ha sido explotada para crear algoritmos computacionales simples, por ejemplo mediante el recocido simulado, para maximizar la modularidad. La forma general de la modularidad para un número arbitrario de las comunidades es equivalente a un vidrio de espín Potts y algoritmos similares puede ser desarrollado para este caso también. [5]

Límite de resolución

La modularidad compara el número de enlaces dentro de un grupo con el número esperado de enlaces que uno encontraría en el grupo si la red fuera una red aleatoria con el mismo número de nodos y donde cada nodo mantiene su grado, pero los enlaces son lo contrario adjunta al azar. Este modelo nulo al azar asume implícitamente que cada nodo puede quedar unido a cualquier otro nodo de la red. Tal suposición es razonable sin embargo si la red es muy grande, como el horizonte de un nodo incluye una pequeña parte de la red, haciendo caso omiso de la mayor parte de ella. Por otra parte, esto implica que el número esperado de enlaces entre dos grupos de nodos disminuye si el tamaño de la red aumenta. Así, si una red es lo suficientemente grande, el número esperado de enlaces entre dos grupos de nodos en modelo nulo de modularidad puede ser menor que uno. Si esto sucede, un solo borde entre los dos grupos sería interpretado por la modularidad como un signo de una fuerte correlación entre los dos grupos, y la optimización de la modularidad conduciría a la fusión de los dos grupos, independientemente de las características de la agrupación. Por lo tanto, incluso débilmente interconectado gráficos completos, que tienen la densidad más alta posible de los enlaces internos, y representan las mejores comunidades identificables, se fusionara por optimización modularidad si la red es suficientemente grande. [6] Por este motivo, la optimización de la modularidad en redes grandes sería un fracaso para resolver las pequeñas comunidades, incluso cuando están bien definidos. Este sesgo es inevitable para los métodos como la optimización de la modularidad, que se basan en un modelo nulo global. [7]

Métodos multirresolución

Hay dos enfoques principales que tratan de resolver el límite de resolución en el contexto modularidad : la adición de un r resistencia a todos los nodos, en la forma de un auto -loop, lo que aumenta (r> 0) o disminuye (r < 0) la aversión de los nodos a las comunidades de formulario ; [8] o la adición de un parámetro γ > 0 en frente del término nulo caso en la definición de la modularidad, que controla la importancia relativa entre los enlaces internos de las comunidades y el modelo nulo. [5] modularidad Optimización para los valores de estos parámetros en sus respectivos rangos adecuados, es posible recuperar toda la mesoescala de la red, desde la macroescala en la que todos los nodos pertenecen a la misma comunidad, a la microescala en el que cada nodo forma su propia comunidad, por lo tanto, los métodos de varias resoluciones de nombres. Sin embargo, se ha demostrado recientemente que estos métodos son intrínsecamente deficiente y su uso no producirán soluciones fiables. [9]

Referencias

1.  Jump up to:Newman, M. E. J. (2006). "Modularity and community structure in networks". Proceedings of the National Academy of Sciences of the United States of America 103 (23): 8577–8696. arXiv:physics/0602124. Bibcode:2006PNAS..103.8577N.doi:10.1073/pnas.0601602103. PMC 1482622. PMID 16723398.
2. Jump up Newman, M. E. J. (2007). "Mathematics of networks". In Palgrave Macmillan, Basingstoke. The New Palgrave Encyclopedia of Economics (2 ed.).
3. Jump up Remco van der Hofstad (2009). "7". Random Graphs and Complex Networks. 
4. Jump upClauset, Aaron and Newman, M. E. J. and Moore, Cristopher (2004). "Finding community structure in very large networks". Phys. Rev. E 70 (6): 066111. arXiv:cond-mat/0408187. Bibcode:2004PhRvE..70f6111C. doi:10.1103/PhysRevE.70.066111.
5. Joerg Reichardt and Stefan Bornholdt (2006). "Statistical mechanics of community detection". Physical Review E 74 (1): 016110. arXiv:cond-mat/0603718. Bibcode:2006PhRvE..74a6110R. doi:10.1103/PhysRevE.74.016110.
6. Jump up Santo Fortunato and Marc Barthelemy (2007). "Resolution limit in community detection". Proceedings of the National Academy of Sciences of the United States of America 104 (1): 36–41. arXiv:physics/0607100. Bibcode:2007PNAS..104...36F.doi:10.1073/pnas.0605965104. PMC 1765466. PMID 17190818.
7. Jump upJ.M. Kumpula, J. Saramäki, K. Kaski , and J. Kertész (2007). "Limited resolution in complex network community detection with Potts model approach". European Physical Journal B 56 (1): 41–45. arXiv:cond-mat/0610370. Bibcode:2007EPJB...56...41K.doi:10.1140/epjb/e2007-00088-4.
8. Jump up Alex Arenas, Alberto Fernández and Sergio Gómez (2008). "Analysis of the structure of complex networks at different resolution levels". New Journal of Physics 10 (5): 053039. arXiv:physics/0703218. Bibcode:2008NJPh...10e3039A. doi:10.1088/1367-2630/10/5/053039.
9. Jump up Andrea Lancichinetti and Santo Fortunato (2011). "Limits of modularity maximization in community detection". Physical Review E 84: 066122. arXiv:1107.1155. Bibcode:2011PhRvE..84f6122L. doi:10.1103/PhysRevE.84.066122.

Wikipedia