¿Es para tanto? ¿Vos que opinás?

Este blog reúne material del curso de posgrado "Análisis de redes sociales" dictado en la Universidad Nacional del Sur (Argentina).




 |
| El grafo completo K5. En un subgrafo como éste, los vértices forman un clique de tamaño 5. |
 |
| Los nodos 1,2 y 5 forman un clique |
 Google ordena los resultados de la búsqueda utilizando su propio algoritmo PageRank. A cada página web se le asigna un número en función del número de enlaces de otras páginas que la apuntan, el valor de esas páginas y otros criterios no públicos.
Google ordena los resultados de la búsqueda utilizando su propio algoritmo PageRank. A cada página web se le asigna un número en función del número de enlaces de otras páginas que la apuntan, el valor de esas páginas y otros criterios no públicos. es el PageRank de la página A.
es el PageRank de la página A.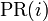 son los valores de PageRank que tienen cada una de las páginas i que enlazan a A.
son los valores de PageRank que tienen cada una de las páginas i que enlazan a A.rel="nofollow" como un intento de luchar contra el spam. De esta forma cuando se calcula el peso de una página, no se tienen en cuenta los links que tengan este atributo.






 tiene
tiene  vecinos; entonces un máximo de hasta
vecinos; entonces un máximo de hasta  enlaces pueden existir entre ellos (esto ocurre cuando cada vecino de
enlaces pueden existir entre ellos (esto ocurre cuando cada vecino de  está conectado a cada otro vecino de
está conectado a cada otro vecino de  ). Sea
). Sea 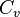 la fracción de estos enlaces permitidos que existen actualmente. Definamos
la fracción de estos enlaces permitidos que existen actualmente. Definamos  como el promedio de
como el promedio de 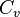 sobre todos los
sobre todos los  ."
.".png)
 formalmente consiste de un conjunto de vértices
formalmente consiste de un conjunto de vértices  y un conjunto de enlaces
y un conjunto de enlaces  entre ellos. Un enlace
entre ellos. Un enlace 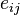 conecta al vértice
conecta al vértice  con el vértice
con el vértice 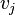 .
. para un vértice
para un vértice  es definido como sus vecinos inmediatamente conectados como sigue:
es definido como sus vecinos inmediatamente conectados como sigue:
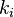 como el número de vértices,
como el número de vértices,  , en el vecindario,
, en el vecindario,  , de un vértice.
, de un vértice. para un vértice
para un vértice  es entonces dado por la proporción de enlaces entre los vértices dentro de su vecindario dividido por el número de enlaces que podría potencialmente existir entre ellos. Para un grafo dirigido,
es entonces dado por la proporción de enlaces entre los vértices dentro de su vecindario dividido por el número de enlaces que podría potencialmente existir entre ellos. Para un grafo dirigido, 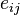 es distinto de
es distinto de  , y por lo tanto para cada vecindario
, y por lo tanto para cada vecindario  hay
hay  enlaces que podrían existir entre los vértices dentro del vecindario (
enlaces que podrían existir entre los vértices dentro del vecindario (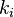 es el número de vecinos de un vértice). Entonces, el coeficiente de agrupamiento local para grafos dirigidos está dado por [2]
es el número de vecinos de un vértice). Entonces, el coeficiente de agrupamiento local para grafos dirigidos está dado por [2]
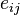 y
y  son idénticos. Por ello, si un vértice
son idénticos. Por ello, si un vértice  tiene
tiene 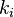 vecinos,
vecinos, 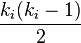 enlaces podrían existir entre los vértices dentro de su vecindario. Por ello, el coeficiente de agrupación local para grafos no dirigidos puede ser definido como
enlaces podrían existir entre los vértices dentro de su vecindario. Por ello, el coeficiente de agrupación local para grafos no dirigidos puede ser definido como
 el número de triángulos sobre
el número de triángulos sobre  para un grafo no dirigido
para un grafo no dirigido  . Esto es,
. Esto es,  es el número de subgrafos de
es el número de subgrafos de  con 3 enlaces y 3 vértices, uno de los cuales es
con 3 enlaces y 3 vértices, uno de los cuales es  . Sea
. Sea 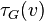 el número de of tripletes sobre
el número de of tripletes sobre  . Esto es,
. Esto es, 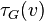 es el número de subgrafos (no necesariamente inducidos) con 2 enlaces y 3 vértices, uno de los cuales es
es el número de subgrafos (no necesariamente inducidos) con 2 enlaces y 3 vértices, uno de los cuales es  y tal que
y tal que  es incidente a ambos enlaces. Entonces podemos también definir al coeficiente de agrupamiento como
es incidente a ambos enlaces. Entonces podemos también definir al coeficiente de agrupamiento como 

 se encuentra también conectado a cada otro vértice dentro del vecindario, y 0 si ningún vértice conectado a
se encuentra también conectado a cada otro vértice dentro del vecindario, y 0 si ningún vértice conectado a  se conecta con ningún otro vértice que está conectado a
se conecta con ningún otro vértice que está conectado a  .
. :[7]
:[7]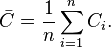
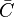 es significativamente más alto que un grafo aleatorio construido con el mismo conjunto de vértices y si el grafo tiene aproximadamente la misma longitud media de camíno más corto que si correspondiente grafo aleatorio.
es significativamente más alto que un grafo aleatorio construido con el mismo conjunto de vértices y si el grafo tiene aproximadamente la misma longitud media de camíno más corto que si correspondiente grafo aleatorio.